A Subtraction Triangle is sort of like Pascal's Triangle, with some obvious differences. To begin with, it will appear on your screen as a "top down" triangle, with the vertex at the bottom. Secondly, it is formed not with addition (you can create Pascal's Triangle by adding two adjacent numbers and putting their sum in the position below and between the two numbers) but with subtraction.

An example of a Subtraction Triangle is shown below. Note that each of the red numbers is the positive difference between the two numbers above it (Example: 6 - 3 = 3, 6 - 2 = 4, and 2 - 1 = 1).
 

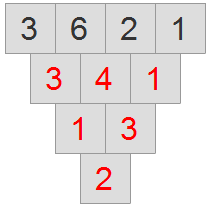
When you begin playing the game, your Triangle is scrambled. As you can see from the image below, the numbers do not follow the rules for a Subtraction Triangle. 
 

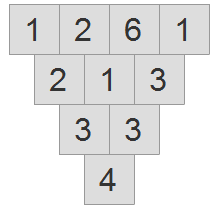
Your job is to rearrange the numbers so they conform to the Subtraction Triangle rules. To do this, simply click on a number tile, and then click the location where you want to move it. The two numbers you have clicked will change locations. If any of the tiles are now the difference of the two numbers above them, they will turn green. The following images shows the game board after swapping the four at the bottom with the one two rows above it.
 

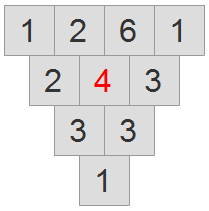
The game continues until all the numbers below the top row are green, indicating that all the numbers are properly placed. Note: there may be more than one possible solution for some puzzles.
 

Difficulty Level

The images shown above are from an easy game. Choose "Easy" if you want to play a game consisting of four rows. For a more challenging game, select "Difficult," which gives you a five row game!

As with many other games on this site, the term "Easy" is a relative term; while the "Easy" puzzles are much less difficult than the "Difficult" puzzles, you may still find them challenging!
 

Game Trivia

The game database contains 1000 different puzzles. All of these are "Difficult" puzzles. When you choose "Easy," the site takes a "Difficult" game and fills in the top row, then hides that row from your view and scrambles the remaining numbers. The result is a four row puzzle.