Polygon Diagonals

Reference > Mathematics > Geometry > Polygons

A diagonal is a line segment which connects two non-adjacent vertices of a polygon.

Why do we specify non-adjacent? Because if you connect two adjacent vertices, that's just a side of the polygon, not a diagonal!

Can we figure out how many diagonals a polygon has? Of course we can. Let's begin with a specific example, and then we'll use that to help us develop a formula.

Let's take the nonagon below. How many diagonals does it have?

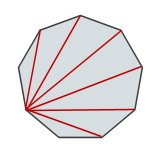
To start figuring it out, let's pick a vertex, and draw all of the diagonals from that vertex to all the other vertices. How many are there? Well, we can't draw a diagonal from a vertex to itself, and we can't draw a diagonal to either of the two adjacent vertices, so that's three vertices we can't draw diagonals to. Since there are 9 vertices in all, that's a total of 9 - 3 = 6 diagonals we can draw:

Since there are nine vertices, we should be able to do this nine times, right? Here the green lines represent diagonals drawn from another vertex.

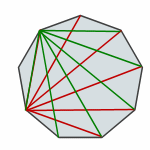
But wait a minute! Did you notice that we've drawn a diagonal twice? There's one diagonal that's been drawn both red and green (it looks kind of grayish in the picture)!

It turns out that if we draw diagonals from every vertex, we'll have counted every diagonal twice. But that's no problem--we can take our total and divide it by two to get the result.

So from every vertex we can draw 6 diagonals, and we can do this from all 9 vertices for a total of 54 diagonals. But since we've counted each one twice, it's really 54 divided by 2, or 27.

Generalizing for an n-gon
If you look at our example for a 9 sided figure, you can see how we used the number 9 in our figuring, and we can just substitute n in its place to find the number of diagonals in an n-gon:

d = ¹/₂n(n-3)