A trapezoid is a quadrilateral in which exactly one pair of opposite sides is parallel.

In the definition above, it's important to note the word exactly. If a quadrilateral has two pairs of parallel sides, it is not a trapezoid. Instead, it is called a parallelogram, which we'll learn about on another page.

Here's a picture of a trapezoid:
 

In the picture shown above, you can see that there are two horizontal sides; these are the two sides that are parallel, and they are called the bases of the trapezoid. Yes, a trapezoid has two bases. In this picture you can see that the two bases have unequal lengths. In a trapezoid, the bases are never congruent. We usually call them b₁ and b₂.

A trapezoid also has a height (or altitude); if you drew a line segment perpendicularly from one base to the other, the length of that segment is the altitude of the trapezoid.

Like rectangles, triangles, circles, and other closed figures, the trapezoid has an area, and it can be found using the following formula:

A = ¹/₂(b₁ + b₂) x h

If you're like me, you don't like memorizing formulas, so I'll give this to you in words:

The area of a trapezoid is the average of the bases, times the height.
 

Special Trapezoids

A right trapezoid is a trapezoid in which one of the sides is perpendicular to the two bases:
 

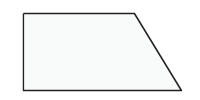
In this special case, if you know the length of the perpendicular side, that's the same as the altitude of the trapezoid.

 

An isosceles trapezoid is a trapezoid in which the two non-parallel sides are congruent. In an isosceles trapezoid, the angles come in congruent pairs, just like in an isosceles triangle.

I won't prove that for you, but the proof isn't hard. Imagine extending the sides of the trapezoid until they form a triangle:
 

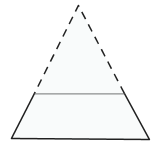
Now think about what you know of isosceles triangles, parallel lines, and triangle similarities. What you'll conclude is that the entire triangle is similar to the smaller one, and that the smaller triangle is isosceles, which makes the bigger triangle isosceles too.

If you construct the two diagonals of the trapezoid, they are congruent if and only if the trapezoid is isosceles.

Studying the picture above may also help you realize something else about trapezoids: the angles at the bottom bases are supplementary to the angles at the top bases--and that's not just true of isosceles trapezoids! 

1.

Why aren't the bases of a trapezoid ever congruent?

2.

The bases of a trapezoid have lengths 12 and 10, and its height is 9. What is the area?

3.

The area of a trapezoid is 45, and its height is 5. What is the sum of its bases?

4.

In a right trapezoid, the bases have lengths 5 and 7. The other two sides have lengths 4 and 6. What is the area of the trapezoid?

5.

Two of the angles of a trapezoid are 60 and 140. What are the other two angles?

6.

The angles of a trapezoid are 45, 45, 135, and 135. What can you conclude about the diagonals of the trapezoid?

7.

In the trapezoid of the previous problem, the bases of the trapezoid are 10 units and 16 units. What is the area of the trapezoid?