Two Body Problems

A type of problem which frequently is encountered has two objects connected together with a force applied to one of them.  Additional complications may be produced by including considerations of friction forces.  A typical problem of this type might be one object resting on a horizontal surface with a specified coefficient of friction connected to another object by a string passing over a pulley.  The object hanging from the string is released and the force of gravity acting on it causes both objects to accelerate.  To solve these problems, draw a separate diagram of each object showing all forces acting on it.  Represent any unknown force (frequently the force between the two objects) with a variable.  Write a Newton's second law equation for each object.  Solve the system of equations. Study the example in the sample problem section.

Sample Problem #1

A 0.5 kg object rests on a table.  The coefficient of friction between the object and the table is 0.3.  It is connected by a massless string passing over a massless frictionless pulley to a 0.75 kg object which is released and allowed to fall, pulling the first mass after it.  Calculate the acceleration of the system and the tension in the string.

Sample Solution #1

Draw a neat diagram showing both objects and any forces known.  Also, draw a sketch of each object by itself to show the forces acting on that object only as in Figure 2.4.1 

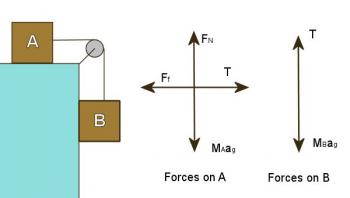
^{Figure 2.4.1}

Study the free body diagrams above  carefully.  Note that the force upward on B is equal to the force that pulls forward on A.  Since A and B are connected together their accelera­tions will be the same.  Actually this is not true at the very instant that the system is released since the string is stretched and the amount of stretch will change slightly as the system starts to move.  However, for the present we will skip this transient condition.

The friction force on object A can be found by applying Equation 4, F_f = μF_N.  The normal force in this situation is the weight of object A.  The mass of object A is .5 kg (500 g) so its weight is 0.5a_g = 4.9 N.  The force of friction can now be found to be 1.47 N. The weight of B is 0.75·9.8 = 7.35 N.  This is greater then the friction force so the system will accelerate.

From the free body diagrams we see that the force on  A is T - 1.47 and the force on B is 7.35 - T.  Using these in the mathematical statement of Newton's second law we obtain:

Be sure that you know how these equations were obtained.  Solve the equations to obtain values of 4.7 and 3.8 N for the acceleration and force respectively.

Analyze the results carefully.  The tension in the string is less than the weight of object B, otherwise object B could not accelerate.  The tension is greater than the friction force on object A or that object would not accelerate.  Note also that the acceleration is less than the acceleration of gravity.  This is necessary because there is an upward force of T on object B.  Only if that force were zero would object B be in free fall.  In that case it would fall with the acceleration of gravity.

Another way of approaching the problem is to consider the two coupled objects as one object.  The net force tending to accelerate them is the weight of B minus the friction force holding back object A.  The total mass is 1.25kg.  Therefore, applying Newton's second law we obtain:

Which can be solved to give the same value of a as obtained above.  This might seem to be a little simpler than the preceding method but keep in mind that the force in the connecting rope can not be obtained by this method.  You must consider the forces acting on just one object if you want to find this force.

Diagrams for Problems Below

Problems in the section below reference Figures 2.4.2 through 2.4.5

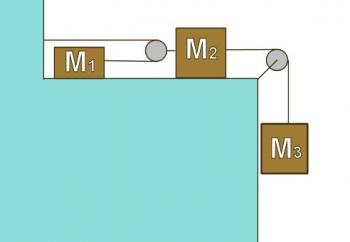
^{Figure 2.4.2}

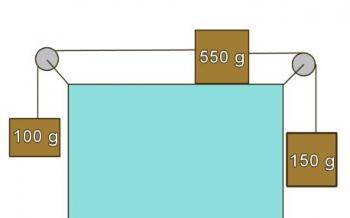
^{Figure 2.4.3}

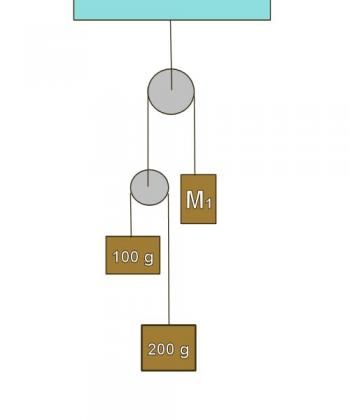
^{Figure 2.4.4}

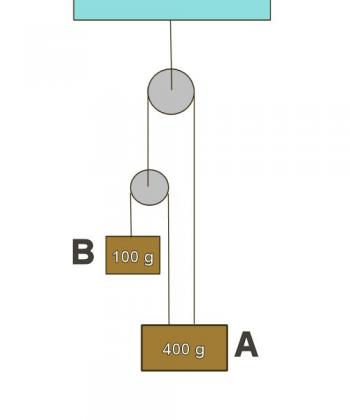
^{Figure 2.4.5}

1.

A 10 kg block rests on a smooth table and is tied to a cord running over a light friction­less pulley to an 6.0 kg block at the lower end of the cord. What will be the acceleration of the system?

2.

In the previous problem, find the tension in the cord between the two objects.

3.

In the arrangement shown in Figure 2.4.2 above, m₁=100 g, m₂=400 g, m₃=200 g, the pulleys are massless, and the surfaces are frictionless. What is the acceleration of m₂?

4.

Calculate the acceleration of the system in Figure 2.4.3 above and the tension in each string if there is no friction in the system.

5.

Two blocks are hung from the ends of a rope that goes over a pulley. The mass of block A is 10 kg, and the mass of block B is 9.0 kg. What is the resulting acceleration and what is the tension in the rope?

6.

In Figure 2.4.4 above, what should be the value of M₁ such that the 100 g mass does not move? If M₁ has this value, what is its acceleration?

7.

Find the accelerations of the masses A and B in Figure 2.4.5 above, and the tension in the cords.