|
|
 The Golden Ratio as a Continued FractionThis page (and the next one) could easily fit in the Slick Math! section of the site, because they have math problems which, at a glance, look fairly intimidating, but are actually quite simple and elegant to solve. They are here instead, because they involve The Golden Ratio.Take a look at the following continuing fraction (the fraction continues on infinitely in the denominator).  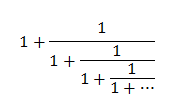How in the world shall we solve such a bizarre looking mess? Well, it's not as hard as it might look at first glance. Let's start by setting that expression equal to R. 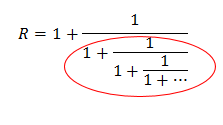Notice, now that the part of the expression which is circled in red is identical to the entire expression:  From this we conclude that: R = 1 + 1/R. This can be manipulated to create a quadratic equation: R2 - R - 1 = 0. That quadratic might not look familiar to you, but you should get used to it, because you'll see it again and again when you're dealing with The Golden Ratio. In fact, do you remember seeing this equation on the first page?  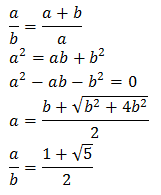If you set b equal to one, you get exactly the same quadratic as the one I just showed you, and you see that the value of the continued fraction is φ, or The Golden Ratio! On the next page, we'll take a look at a continued radical expression which evaluates in the same way.
Contents copyright 2008 by Douglas Twitchell. Contents of this page may not be reproduced without permission of the author. Go On A Quest!
Site Features
|
|||||||||||||||||||||||||||||||||
