Vertical Stacker
Professor Puzzler's Vertical Stacker
The Vertical Stacker is one of Professor Puzzler's Perspective Calculators.This calculator will allow you to take a plane drawn in perspective, and divide the height into n vertically-stacked regions that are of equal width. For example, suppose you are drawing a building, and one wall has 8 columns evenly spaced down the length of the wall. You can't evenly space the columns in your drawing; the spaces in the distance must be smaller than the ones in the foreground.
Instructions
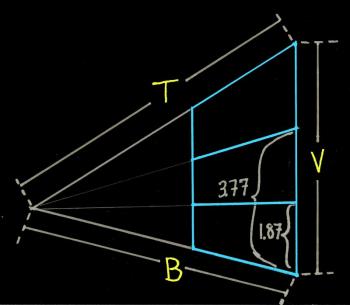
Refer to the diagram below to understand the information needed by the calculator. The diagram is a sample that uses the default values which appear in the calculator.
- The cyan region represents the rectangular plane surface you want to divide into equal regions that are stacked vertically.
- Select the vertical side further away from the vanishing point.*
- T: The "top length" is the distance from the vanishing point to the top endpoint of the vertical segment you wish to divide into equal segments.
- B: The "bottom length" is the distance from the vanishing point to the bottom endpoint of the vertical segment.
- V: The "vertical length" is the length of the segment that you wish to n-sect.
- N: The number of vertically stacked regions. In the sample image, N = 3
- Once you have the values from the calculator, measure up from the bottom of the vertical side.
* Do you have to use the side furthest from the vanishing point? No, you do not. You can use the closer one. However, the closer side is shorter, which means you may not get as much precision by using that side.
What's the Point?
Suppose you are drawing a building. Odds are good you're going to need to divide that building's wall into evenly spaced regions stacked vertically. Why? Well, if the building is made of bricks, or it's a log cabin, or it has siding, each row of brick/rock/wood/siding has to have the same height. It's tempting to assume that you can just measure your vertical side, divide that into n equal pieces, and be done. However, it's not the side that's getting n-sected; it's the angle at the vanishing point. This calculator works out the trigonometry for you so you don't have to use a protractor to try to n-sect an angle.
Doing the Math
We begin by using the law of cosines to calculate the cosine of the angle at the vanishing point, then we calculate the angle using the inverse cosine function. We do the same to calculate the angle at the bottom.
Then the vanishing point angle is n-sected (divided by n). Now we can calculate the missing angles in the triangles formed by the bottom side, the vertical side, and the n-sector rays.
Finally, since we have all the angles of the triangles, and we have a side, we can use the law of sines to calculate the missing side.
Blogs on This Site
Like us on Facebook to get updates about new resources