Theorem of Pappus
The Theorem of Pappus states that when a region R is rotated about a line l, the volume of the solid generated is equal to the product of the area of R and the distance the centroid of the region has traveled in one full rotation. The centroid of a region is essentially the one point on which the region should "balance." The centroid of a rectangle with vertices (0,0), (x,0), (0,y), and (x,y) is the point (x/2,y/2), for example, but finding the centroid of a non-rectangular region is a little bit trickier. Part of this week's problem will require you to come up with a unique way of locating the centroid of a semicircle.
Consider the figure below, a rectangle topped by a semicircle.
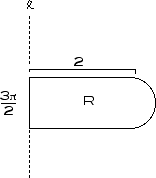
Use the Theorem of Pappus to:
1) Find the centroid of the semicircle and use it to find the volume of the solid generated when just the semicircle is rotated about l.
2) Find the volume of the solid generated when just the rectangle is rotated about l.
3) Find the distance from the centroid of the region R to l.
The Theorem of Pappus states that when a region R is rotated about a line l, the volume of the solid generated is equal to the product of the area of R and the distance the centroid of the region has traveled in one full rotation. The centroid of a region is essentially the one point on which the region should "balance." The centroid of a rectangle with vertices (0,0), (x,0), (0,y), and (x,y) is the point (x/2,y/2), for example, but finding the centroid of a non-rectangular region is a little bit trickier. Part of this week's problem will require you to come up with a unique way of locating the centroid of a semicircle.
Consider the figure below, a rectangle topped by a semicircle.

Use the Theorem of Pappus to:
1) Find the centroid of the semicircle and use it to find the volume of the solid generated when just the semicircle is rotated about l.
2) Find the volume of the solid generated when just the rectangle is rotated about l.
3) Find the distance from the centroid of the region R to l.




