In this reading we will explore the angles of polygons. You may remember from the Quadrilateral readings that the sum of the interior angles of a quadrilateral is 360 degrees. You also should remember that the sum of the angles of a triangle is 180 degrees. 

3 sides => 180 degrees
4 sides => 360 degrees
5 sides => ___ degrees

Do you have a guess how to fill in the blank? A good guess might be 540, since it forms a nice pattern, with a difference of 180 degrees between each pair of numbers in the list. Well, it turns out 540 is correct. Take a look at the image below to see why:
 

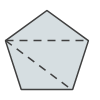
I'm able to split the pentagon into three triangles, and each of those triangles has a total of 180 degrees, so the pentagon must have 3 x 180 = 540 degrees on its interior angles.

What about a hexagon? How many triangles can you split a hexagon into? You can split it into 4 triangles, which means the sum of its angles is 4 x 180 = 720 degrees!

It turns out that if a polygon has n sides, you can split it into n - 2 triangles, so the sum of its interior angles is:

180(n-2)
 

Interior Angles of Regular Polygons

Remember that a regular polygon is a polygon in which all the interior angles are congruent. So if we know the sum of the interior angles, we just need to divide that sum by the number of sides to find out the measure of any angle of the polygon:

180(n-2)/n
 

Exterior Angles

Just like quadrilaterals, all polygons have exterior angles. The image below shows the exterior angles of a regular pentagon.

 

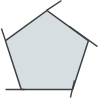
Remember that the exterior angles are the angles that are supplementary to the interior angles. Can we figure out the sum of the exterior angles? Of course we can!

Since every exterior angle is supplementary to the corresponding interior angle, and there are n such pairs (where n is the number of sides in the polygon), the total of all the interior and exterior angles together is 180n.

But we just figured out that the sum of all the interior angles is 180(n - 2), so the sum of all the exterior angles must be:

180n - 180(n - 2) = 360 degrees!

So it turns out that it doesn't matter how many sides the n-gon has; the sum of the exterior angles is always 360.

And if the polygon is regular? Well, then all the exterior angles are the same size, so each one has a measure of:

360/n.

1.

How many triangles can we divide a decagon into?

2.

What is the sum of the measures of the interior angles of a heptagon?

3.

If a nonagon is regular, what is the measure of each of its interior angles?

4.

If the sum of the interior angles of an n-gon is 2,340 degrees, what is the value of "n"?

5.

One polygon has two more sides than another. Together, the sum of their interior angles is 3,600 degrees. How many sides do the two polygons have?

6.

A polygon has 15 sides. What is the average of the measures of its exterior angles?

7.

The measures of the interior angles of a pentagon are in the ratio 1:1:1:2:3. What is the measure of the largest angle?

8.

Fully classify the polygon in the previous question.

9.

If the measures of the interior angles of an n-gon average 120, what is the average of the exterior angles?

10.

The measures of the exterior angles of a regular polygon are 7.5 degrees. How many sides does the polygon have?