If a polygon is regular, there is a point which we can define as the center. It is the point which is equidistant from each vertex.
 

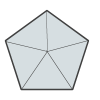
In the figure above, the line segments from the center to the vertices divide the pentagon into five congruent triangles. Do you know what the measure of the angle at the center is? It's 72 degrees. Do you know how I figured that out?

Well, there's a total of 360 degrees all the way around the center, and it's split up into 5 equal angles, so each angle has a measure of 360 / 5 = 72 degrees!

Now suppose you dropped a line segment from the center of the pentagon shown above to the midpoint of a side, as shown below.
 

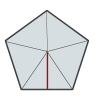
The red line segment is called an apothem. Now, if you were interested in doing some proofs, you could prove some interesting things. For example, SSS Theorem helps you prove that the apothem cuts that triangle into two congruent triangles. From this you can conclude that the apothem bisects the central angle, and it is perpendicular to the side.

The important information here is that the apothem is perpendicular to the side. Why is it important? Because that means it's the height of the triangle formed by two vertices of the polygon and its center.

If you know some basic triangle geometry, you know that this means that the area of the triangle is¹/₂sa, where s is the length of a side of a polygon, and a is the length of its apothem.

But wait! This pentagon has 5 such triangles, so if we multiply that by 5, we have the area of the pentagon!

We can turn this into a formula, recognizing that where we used the number 5, we need to replace it with n for the number of sides:

A = ¹/₂nsa

But suppose you weren't given the side length - suppose instead you were given the perimeter. Well, that's not a big deal, because you can divide the perimeter by n to get a side...but wait a minute...that just simplifies to:

A = ¹/₂pa

There is a specific relationship between s, n and a, which we won't deal with in detail, since it involves trigonometry. If you know trigonometry, a challenge exercise is to find a formula that relates the three variables s, n and a.

1.

How many apothems does a nonagon have?

2.

If a square has sides of length 2, what is the length of its apothem?

3.

If a regular octagon is divided into n triangles as shown for a pentagon, what is the measure of the central angle of each triangle?

4.

In the previous question, how big are the other two angles of each triangle?

5.

When a regular hexagon is divided into triangles as shown above for a pentagon, what kind of triangle is each triangle?

6.

If the perimeter of a regular polygon is 36 units, and the length of the apothem is 5.196, what is the area of the polygon?

7.

The area of a regular polygon is 81 square units, and the length of its apothem is 4.5 units. What is the perimeter of the polygon?

8.

A regular heptagon has sides of length 10 units. The length of its apothem is 20.8 units. What is the area of the heptagon?

9.

Trig challenge: can you find a formula that relates n, s and a?