"A quadrilateral is a closed figure which is bounded by four straight line segments."

If you start with that simple definition, you should be able to picture all kinds of things that are quadrilaterals:
 

• a ceiling
• a sheet of paper
• a kite

Quadrilaterals come in all shapes and sizes. Some of them have special names like "square," "rectangle," "parallelogram," "rhombus," and "trapezoid."
 

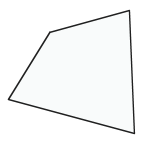
For this reading, we're going to talk very generally about quadrilaterals, so we'll start with a quadrilateral that isn't any of those "special" cases mentioned above.

Did you know that in any quadrilateral, the sum of the inside angles equals 360 degrees? That's not all that difficult to prove. We won't formally prove it, but I can show you a picture that'll help you to believe it:
 

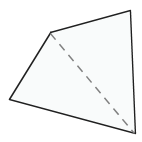
In this diagram, the quadrilateral is divided into two triangles. We don't know much about those triangles--we don't even know if they are congruent to each other. But what we do know is that the sum of their interior angles is 180 degrees. And since there aretwo of them, the total of all their angles is 360 degrees.

Quadrilaterals don't just have interior angles; they also have exterior angles. The exterior angles are the angles you create by extending the sides of the quadrilateral:
 

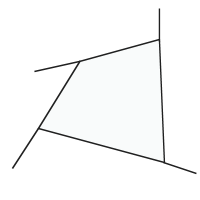
Now, if you're paying attention, you might think, "But that's only half of the exterior angles! You can extend the sides in the other direction too!"

Right you are! But if you'll stop to think about it for a second (and if you remember your vertical angle theorem) you'll realize that those exterior angles are the same size as the ones drawn. So usually we just think about exterior angles going in one direction (clockwise or counter-clockwise) and remember that there are four more going in the other direction.

Unless a quadrilateral is a "special" quadrilateral like a rectangle or a square, we don't know much about the exterior angles. Except we do know this: they add up to 360 degrees.

How do we know this? Simple. Every interior and exterior angle forms a supplementary pair, so if you add all the interior angles and all the exterior angles, you'll get 4 straight lines, or 720 degrees. But since the sum of the interior angles is 360 degrees, that means the sum of the exterior angles is 720 - 360 = 360 degrees!

"But hang on a second," you might think, "That's all well and good for a quadrilateral like the one you've drawn there, but not all quadrilaterals look the same. Some of them have a squished-in angle..."

A concave quadrilateral? Like this one?
 

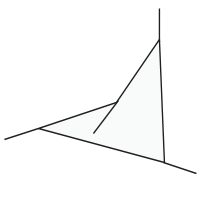
"Exactly! You can't tell me that the exterior angles of that thing add up to 360 also!"

Well, it turns out that, since one of the "exterior" angles is actually on the interior, we can still make this work, as long as we agree that whenever an exterior angle is on the interior, we're going to say it has a negative degree measure.

So yes, even for concave quadrilaterals, the sum of the exterior angles is 360 degrees.

1.

Name three real-world objects (besides the ones mentioned in this reading) that are quadrilaterals.

2.

In a quadrilateral, three of the angles are 90, 110, and 40 degrees. What is the size of the other angle?

3.

If all the angles of a quadrilateral are equal, how big is each angle?

4.

The angles of a quadrilateral are in the ratio 1:2:3:4. What are the angle measures?

5.

If an interior angle of a quadrilateral is 45 degrees, what is the measure of the corresponding exterior angle?

6.

If the exterior angles of a quadrilateral are in the ratio 2:3:5:5, what are the measures of the interior angles?

7.

Three of the interior angles of a quadrilateral measure 100, 150, and 20. What are the measures of the exterior angles?

8.

Three of the exterior angles of a quadrilateral are 120, 150, and 140. How can you tell that this quadrilateral is concave?

9.

None of the four angles of a quadrilateral are congruent. Can any of the exterior angles be congruent? Why, or why not?