A rhombus is a parallelogram in which all the sides are equal.

If you want to picture a rhombus, imagine the "diamond" shape on a playing card. The opposite sides are parallel, and all four sides are the same length.

Or, you can picture a square. A square is a special type of rhombus in which all the angles are 90 degrees. 

Since a rhombus is a parallelogram, and a parallelogram is a kind of quadrilateral, that means that all the properties of quadrilaterals are also true of rhombuses, as are the properties of parallelograms. In addition, we have some more special properties:

Perpendicular Diagonals: The diagonals of a rhombus don't just intersect each other, they are also perpendicular to each other.

Congruent Triangles: Remember that in a parallelogram, the diagonals split the parallelogram into two pairs of congruent triangles? Well, in a rhombus, the diagonals split the rhombus into four congruent triangles. Yes, that's right, all four of those little triangles are congruent.

 

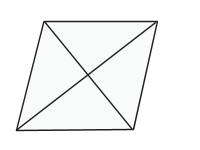
Bisected Angles: In a parallelogram, the diagonals bisect each other, but in a rhombus, they also bisect the angles of the rhombus.

Inscribed Circle: This is something new - the rhombus is the first kind of quadrilateral we've talked about that it is guaranteed that you can construct a circle that's tangent to all four sides. This is true of every rhombus.

Area: The rhombus has an area equal to half the product of its diagonals. This is not hard to prove; one diagonal (p) splits the rhombus into two congruent triangles, and the altitude of each of them is half the other diagonal (q/2), which leads to an area of: 

¹/₂pq

1.

Which of the following is true: "All rhombuses are parallelograms," or "All parallelograms are rhombuses?"

2.

Which of the following is true: "All rhombuses are squares," or "All squares are rhombuses?"

3.

What is the area of a rhombus if its diagonals have length 6 and 8?

4.

The perimeter of a rhombus is 24 units. What is the length of a side?

5.

What is the length of a side of the rhombus in the previous question? (Hint: remember that the diagonals bisect each other, and are perpendicular to each other, and use the Pythagorean Theorem!)

6.

A diagonal of a rhombus forms a 20 degree angle with a side of the rhombus. What are the angles of the rhombus?