Friction

Friction is a force which opposes motion.  Sliding friction will be caused whenever one surface slides over another.  The following relation gives a good approximation of the amount of sliding friction:

Where F_f is the force of friction,  μ  (the Greek letter mu) stands for the coefficient of friction, and F_N  represents the normal force.  The normal force is the force pressing the two surfaces together.  In this context, the word normal denotes perpendicular; the force is perpendicular to the surfaces.  In the case of an object resting on a horizontal surface with any forces applied parallel to the surface the normal force will be equal to the weight of the object.  Situations where the surfaces are not horizontal or forces are applied at angles to the surface will have to be delayed until after a study of vectors.

The coefficient of friction depends on the nature of the surfaces and is determined experimentally.  The value of μ measured for an object which is sliding is generally quite a bit smaller than the maximum value obtained when an object is at rest, thus we generally specify a static (stationary) and kinetic (sliding) coefficient of friction. The amount of surface area in contact has very little effect on the amount of friction.

Sample Problem #1

A 50kg box rests on a horizontal surface.  The coefficient of friction between the box and the surface is 0.25. Calculate the acceleration produced by a 200N horizontal force.

Sample Solution #1

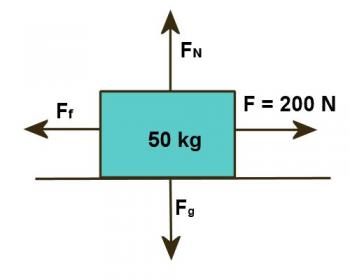
^{Figure 2.3.1}

Study figure 2.3.1.  The force given is not the net force.   To find the net force we must first calculate the friction force and then subtract it from the applied force:

Recall that the force of friction is found by using equation 4:

Before we can use this equation, we must calculate the normal force.  Since the surface  and the applied force are both horizontal, the only vertical force is the weight of the box.  Thus the normal force can be found:

Now the friction force can be found:

The net force must be the difference between the forward force and the friction force or:

Now that we have the net force we can find the acceleration:

Sample Problem #2

A 40kg box rests on a horizontal surface. The static coefficient of friction is 0.4 and the sliding coefficient of friction is 0.25.  A horizontal force is applied to the box.  The force starts at zero and gradually increases until the box just starts to move and is then held constant at that value.  Calculate the force at which the box just starts to move and then calculate the acceleration of the box once it is moving.

Sample Solution #2

     
Find the weight (F_g) of the object:

Find the maximum static friction force:

Since the normal force is the weight we have:

Thus, in order to start the object in motion the applied force must be 157 N.  Actually, it will have to exceed this force momentarily, but we will assume that it then returns to 157 N.

To calculate the acceleration we need the sliding friction force.

The net force is therefore the difference between the applied force and the friction force:

The acceleration can now be found by application of Newton's law:

1.

What horizontal force is necessary to give a block of mass 2.0 kg a horizontal acceleration of 2 , if the block is resting on the floor of an elevator moving downward with an acceleration of 3 ? The coefficient of friction between block and floor is 0.30.

2.

An Eskimo is about to push along a horizontal snowfield a 25 kg sled on which is resting a 35 kg load. The coefficient of kinetic friction between the sled and the snow is 0.1 and the coefficient of static friction between the sled and the load is 0.8. Calculate the maximum acceleration possible for the sled to have without causing the load to slide backward.

3.

For the previous problem, calculate the force needed on the sled to produce this acceleration.

4.

A horizontal force of 100 N is applied to a trunk with a mass of 50 kg. The coefficient of friction between the trunk and floor is equal to 0.10. What is its acceleration?

5.

A hockey player hits a puck and imparts to it a velocity of 8.0 . How far will the puck slide if the coefficient of friction between it and the ice is 0.050?

6.

If the coefficient of friction between a book and a wall is 0.25, how hard would one have to push horizontally in order to hold a 1.25 lb book against a vertical wall without having the book start to slip down the wall?