The principle of conservation of momentum is a direct consequence of Newton's third law.  Newton's third law says that if object A exerts a force on object B then object B will exert an equal force back on object A.  If object A accelerates in one direction B will accelerate in the other.  The accelerations will not necessarily be equal since the masses may be different but since the two forces obviously act for the same time the impulses applied on the two objects are equal and opposite.  Therefore the changes in momentum are also equal and opposite, and the total of the momenta of the two objects will not change.  In this case we say that momentum of the system is conserved.  In general, in any closed system the total momentum of the objects in the system can not change.  Any time one object gains some momentum one way, another object (or combination of objects) gains an equal amount of momentum in the other direction.

It is easy to suggest situations in which it seems that the momentum is not conserved.  For example, a stone thrown vertically upward has an upward momentum which decreases to zero and then increase in the downward direction.  The momentum of the object is clearly not conserved.  The problem here comes because the stone is not a closed system.  To have a closed system we must include the earth with the stone. The same force that acts on the stone slowing its vertical motion acts on the earth, producing an equal change in the momentum of the earth.  The mass of the earth is so large by comparison to that of the stone that its motion seems to be negligible but nevertheless the earth's motion is required by application of the principle of conservation of momentum.

Conservation of momentum is very useful in the solution of problems involving the explosion of an object with small objects flying away in various directions.  When a rifle is fired, the momentum of the bullet is exactly equal and opposite to the recoil momentum of the rifle.  If the respective masses of the objects and the velocity of one of them is known then the velocity of the other can be easily found.

Another useful application of the principle of momentum is in the solution of problems involving collisions between two or more objects.  If the masses of two objects and their velocities before a collision are known, it is possible to calculate the velocity of one of the objects after the collision if the velocity of the other is known.  Note that this does not allow us to determine the final velocity of both objects, we can only find the velocity of one if the velocity of the other is known.

Since momentum is a vector it is possible to have problems where the motion of the objects is not all along a line. In this case it is necessary to calculate components of the momenta of the objects before and after the collision.  The total X‑components before the collision must be equal to the total of the X‑components of the objects after the collision.  In the same fashion the total of the Y‑components must also be the same before and after the collision.

Sample Problem #1

A rifle has a mass of 2 kg and fires a 50 g bullet at a speed of 1000 .  Calculate the recoil velocity of the rifle.

Sample Solution #2

Since the rifle and the bullet form a closed system the total momentum must be the same after firing the gun as before.  The total momentum before is zero so the total after must also be zero.  This will only occur if the momentum of the gun and the momentum of the bullet are equal and opposite.

This is a very simple problem.  The hardest part is recognizing that this problem is going to be solved using the principles of conservation of momentum.  You might question as to whether we have a closed system.  As a matter of fact we do not.  In order to be truly closed we would have to consider the gas involved in the explosion. However, the mass of this gas is so small in comparison to that of the gun and bullet that it may be safely neglected.  You also might question as to whether we need to consider gravity in this problem.  Not really.  The pull of gravity is at right angles to the forces on the gun and bullet so will have no effect on their initial velocities. To be sure, as soon as the bullet leaves the barrel of the gun gravity will give it a downward component of velocity and the earth a corresponding upward component.  However, this does not have any effect on the velocity of the bullet at the instant that it leaves the barrel of the gun.  Air friction will also slow the bullet down but this takes place after we have completed the problem.

Sample Problem #2

A 7 kg object in outer space explodes into 3 fragments.  The masses of the fragments are 3, 2, and 2 kg.  Their velocities all lie in a plane.  The 3 kg mass has a velocity of 10 , and the velocities of the other two objects make angles of 20º and 30º with the velocity of the first.  Calculate the magnitudes of the velocities of the two 2 kg objects.

Sample Solution #2

As seen from the table above and the vector diagrams below, the motion of one of the objects has been placed along the negative x‑axis for convenience. The velocity vectors are shown in figure 5.2.1 and the momenta vectors are shown in Figure 5.2.2.

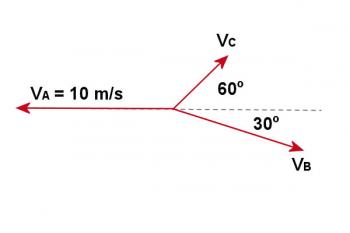
^{Figure 5.2.1}

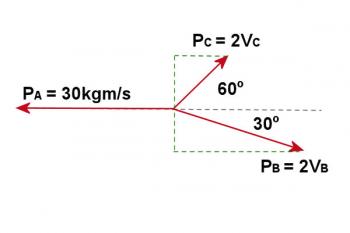
^{Figure 5.2.2}

Since the object was initially at rest, the initial momentum was zero.  After the explosion the total momentum of the three objects must still be zero.  The momentum vectors have been resolved into components which are horizontal and vertical on the page.  Since the total momentum must be zero then the total of the horizontal components must be zero.  Therefore the sum of the two components to the right must be equal to the component to the left as follows:

It is also necessary that there be no component up or down the page, therefore:

The second equation can be solved for V_B to give:

Substituting this in the first equation we obtain:

Solve to obtain:

1.

A 5kg shell is fired vertically upward and explodes at its maximum height of 500m into two fragments of 1kg and 4kg. Both fragments strike the ground at the same instant and the 4kg fragment is observed to strike at a horizontal distance of 35m NE from the point from which it was fired. Where did the other fragment strike? What was the horizontal component of the velocity of the 1kg fragment?

2.

A nucleus, originally at rest, decays radioactively by emitting an electron of momentum 9.22 x 10^-16 g-cm/sec. At right angles to the direction of the electron, a neutrino is emitted with momentum 5.33 x 10^-16 g-cm/sec. In what direction does the residual nucleus recoil? If the mass of the residual nucleus is 3.90 x 10^-22 g, what is its velocity?

3.

A hailstorm has hail falling at an angle of 45 degrees. The individual stones have a mass of 0.1 g and travel with a speed of 7.0 m/sec. 2800 hailstones strike the vertical wall of a barn each second. The barn is 14 m long and 10 m high. What is the change of the horizontal component of momentum in each collision, assuming that the hailstones do not rebound from the wall. What is the total horizontal impulse on the side of the barn in one second? What is the average force on the side of the barn?

4.

A 100g marble strikes a 25g marble lying on a smooth horizontal surface squarely. In the impact the speed of the larger marble is reduced from 100cm/sec to 60cm/sec. What is the speed of the smaller marble immediately after impact?

5.

A 4.0g bullet is fired from a 5.0kg gun with a speed of 600m/sec. What is the speed of recoil of the gun?

6.

A cart of mass 5kg moves horizontally across a frictionless table with a speed of 1m/sec. When a brick of mass 5kg is dropped on the cart, what is the change in velocity of the cart?

7.

Two particles of equal mass and equal but opposite velocities collide. How do the velocities of the two particles after the collision compare with each other?

8.

A 2.0kg ball traveling at a speed of 22m/sec overtakes a 4.0kg ball traveling in the same direction as the first, with a speed of 10m/sec. If after the collision the balls separate with a relative speed of 9.6m/sec, find the speed of each ball.

9.

Two objects of mass 5kg and 10kg have velocities of 2m/sec in the +x direction and 4m/sec in the +y direction. They collide and stick together. What is their final velocity after collision?

10.

A railway gun whose mass is 70 000kg fires a 500kg artillery shell at an angle of 45 degrees and with a muzzle velocity of 200m/sec. Calculate the horizontal recoil velocity of the gun and railway car.