A very important type of collision is one in which the quantity mV² is conserved.  In the next chapter you will find that this quantity is called kinetic energy.  Collisions in which kinetic energy is conserved are called elastic  collisions.  It is not always possible to tell in advance if a collision is elastic or not but the following may give clues.  In elastic collisions the objects never stick together.  Thus a collision of two railroad cars which couple together is not elastic.  A collision in which there is permanent deformation of one or both of the colliding objects is not elastic.  The most nearly elastic collision with which you are probably familiar is the collision between two billiard balls.  Even this collision is not perfectly elastic but is close enough to be considered elastic for most calculations.  Elastic collisions are more common in the subatomic world.  For example, the collision between two protons is usually elastic.  So are collisions between gas molecules.

In working with collisions please keep the following in mind:  Momentum is always conserved.  If you find a situation where it is not then you do not have a closed system.  Some object which you are ignoring is carrying away some momentum.  Kinetic energy is conserved only in elastic collisions.  If objects stick together, are permanently deformed or if heat or some other form of energy is released in a collision, the collision is not elastic. Kinetic energy can remain the same or decrease.  It can never increase in a simple collision.  The only situation in which kinetic energy will increase is when there is an outside source of energy involved such as some kind of explosion, and even in these cases momentum will still be conserved.  It is possible to determine the degree of elasticity of a collision by determining the amount of kinetic energy lost during the collision.

When solving problems involving elastic collisions you must make momentum be conserved in all three directions. This will provide you with 3 equations if the objects involved move in three dimensional space.  In addition kinetic energy, a scalar, is also conserved giving you one additional equation.  Thus it should be possible to solve for as many as four variables.  However, in practice the solution of these equations can be very tedious since they will involve trigonometric relationships.  Therefore you will rarely be asked to complete the solution of a three dimensional elastic collision problem.  However, you should be able to draw the vector diagrams and set up the necessary equations.  Problem 5.6 demonstrates a three dimensional elastic collision problem.

Sample Problem #1

A ball of mass 200 g and with a speed of 50 collides elastically with a ball of mass 400 g.  Both balls move along the same line as the original ball after the collision.  Calculate the speed of both balls after the collision.

Sample Solution #1

First we assign variables to the unknowns.  We will use V_A and V_B for the final velocities of A and B respectively.  Now write an equation for conservation of momentum, keeping in mind that this is a one dimensional collision so there are no components to calculate.  Then write an equation for the conservation of kinetic energy. They are as follows:

Before solving the set of equations notice that one of the equations is a quadratic so you should expect to obtain two sets of solutions.  Be sure not to lose one of them.

When solved the following roots are obtained:

The first set of roots corresponds to the rather uninteresting case where the incoming object misses the stationary object so both objects continue moving as they were.  The second set of answers corresponds to the case where the moving ball hits the stationary ball.  You will note that the speed of the ball A comes out negative indicating that the ball rebounds from the larger ball.  In general, for elastic head on collisions, if the balls are equal in mass the first will stop and the second will carry away all the initial momentum.  If the first is lighter than the stationary ball it will rebound, and if it is heavier than the second it will keep going although with reduced speed and the second will move in the same direction at a higher speed.

Sample Problem #2

In a proton collision with another proton at rest, the first had a velocity of 1 x 10⁷ .  After the collision it went off at an angle of 30º to its original direction.

1. What was its speed after the collision?
2. At what angle and with what speed did the other proton go off?

Sample Solution #2

Examine the diagrams below carefully.  Figure 5.3.1 shows the momenta of the two protons before the collision and figure 5.3.2 shows the momenta after.  In constructing the diagrams the direction of motion of the original proton was chosen as the X‑axis for convenience.

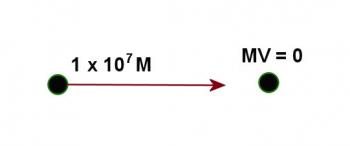
 ^{Figure 5.3.1}

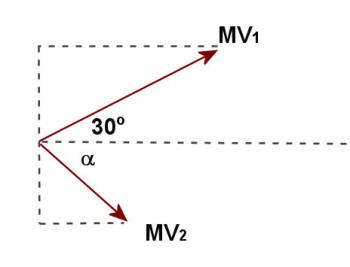
^{Figure 5.3.2}
 
First break the momen­tum vectors into x and y components.  Then write two equations, one for the x-momentum and the other for the y-momentum. These follow:

x-comp

 y-comp

Now write a single equation setting the kinetic energy before equal to the sum of the kinetic energy of the two protons after the collision:

The student will be forgiven if he/she absolutely refuses to work out these equations.  However, for the adventuresome student the answers are:

V₁ = 8.7 x 10⁶
V₂ = 5.0 x 10⁶
α = 60º

1.

A billiard ball moving with velocity v strikes another billiard ball of equal mass, initially at rest. The first ball is deflected at an angle of 30O to its original direction of motion. The second ball moves at a speed of 0.823v after impact What is the velocity (magnitude and direction) of the second ball after collision. Was the collision elastic?

2.

A 10g ball with a velocity of 300cm/sec makes direct impact with a stationary ball of mass 30g. After impact, the velocity of the smaller ball is zero. What is the velocity imparted to the larger ball? What is the fractional loss in kinetic energy?

3.

Oxford Hills is playing Morse in football. A 150‑lb OHHS back dives over the line at a speed of 30ft/sec and is tackled in midair by a 225‑lb linesman moving in the opposite direction at 15ft/sec. What is the speed and direction of both players immediately after impact? (assume they move together after collision) If the time of impact is 1/10sec, what is the average force exerted by one player on the other?

4.

A 1‑lb ball of modeling clay moving northward with a speed of 20ft/sec collides with and sticks to a like ball of clay moving eastward with a speed of 20ft/sec. What is the total momentum of the objects after the collision? How much kinetic energy was lost in the collision?

5.

A billiard ball traveling at a speed of 3m/sec collides with a stationary billiard ball with the same mass and imparts a speed of 1.8m/sec to it. If both balls move in the same direction as the oncoming ball, what is the velocity of the first ball after collision?

6.

A ball of mass 100g traveling with a velocity of 50cm/sec strikes squarely a ball of mass 200g which is at rest. Calculate the final velocities of the balls assuming that the collision was elastic.

7.

A 5kg object is moving to the right with a speed of 2m/sec and collides with a 3kg object moving to the left with a speed of 2m/sec. The objects move together after collision. What is the speed of the system after the collision? How much kinetic energy is lost in the collision?