Addition of Vectors

Addition of vectors is probably the most common vector operation done by beginning physics students, so a good understanding of vector addition is essential.  Study these notes and the material in your textbook carefully, go over all solved problems thoroughly, and work on solving problems until you become proficient.

To add two vectors graphically, construct a vector diagram as follows.  Draw an arrow for the first vector in the proper direction and with a length to some convenient scale.  Start the second vector at the end of the first vector and using a protractor and ruler construct it in the correct direction and of the proper length.  The resultant or sum can then be drawn in as the vector which starts at where the first vector started and ends at the end of the second vector. Refer to Figure 3.2.1.  At the left are shown two vectors A and B.  At the right is a diagram representing the addition of these vectors.  Note that the vectors in the diagram on the right are parallel to and the same length as their counterparts in the diagram at the left.  The total (resultant) is the vector labeled  R.  The magnitude of the resultant can be determined by measuring its length and multiplying by the scale used.  Its direction can be determined with the use of a protractor.

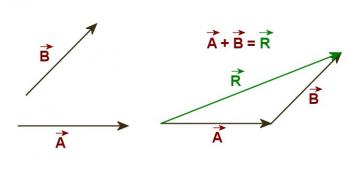
^{Figure 3.2.1}

In theory any two vectors can be added by this method.  It should be  evident that this method is not limited to two vectors.  To add more than 2 vectors just continue the diagram, starting the third vector where the second ends, the fourth at the end of the third and so on.  The resultant will be the vector starting at the beginning of the first vector and ending at the end of the last vector, no matter how many vectors there are in the sum.  Refer to Figure 3.2.2 to see the resultant when 4 vectors A, B, C, and D are added.

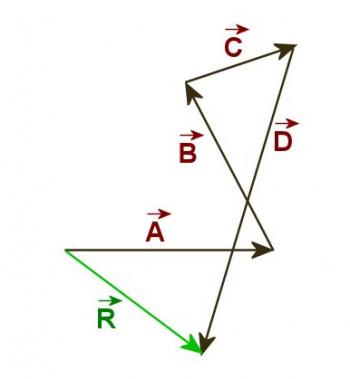
^{Figure 3.2.2}

Since the construction of scale diagrams is tedious and of limited accuracy, it is desirable to develop numerical methods of adding vectors.  The simplest case is the addition of two vectors which make a right angle with each other as in Figure 3.2.3 below. 

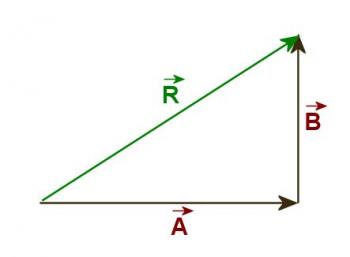
^{Figure 3.2.3}

In this case the resultant, R, forms the hypotenuse of a right triangle.  It is not necessary to draw the triangle to scale since the magnitude of the resultant can be determined mathematically by application of the Pythagorean theorem.  The angle between A and R is arctan(B/A).  (Note: It is possible to determine the angle by using arcsin(R/A) but it is a good practice to avoid the use of a calculated quantity, in this case the value of R.  Instead, find all answers by using given quantities whenever possible.) Therefore if A =300m east and B =400m north then R =500N (square root of 300² + 400² and the angle between A and R is arctan(400/300) = 53.1ºnorth of east.

As a demonstration of adding displacement vectors we will solve the following problem:

Refer to the vector diagram below, Figure 3.2.4. 

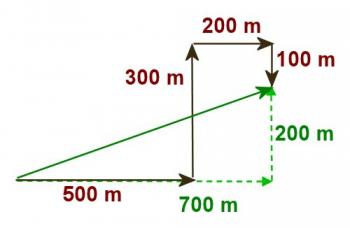
^{Figure 3.2.4}

Note that although this vector diagram has been constructed with the vectors added in the order they were given the same results would be obtained if the vectors were drawn in a different order as shown in Figure 3.2.5. 

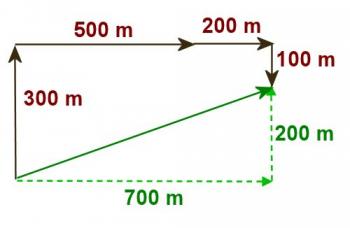
^{Figure 3.2.5}

This illustrates an important property of vectors, addition is commutative.  Now if the eastward displacements are added a net eastward displacement of 700m is obtained.  Since the other two displacements are in the opposite direction they must be subtracted giving a net northward displacement of 200m.  Thus the components of the resultant are 700m east and 200m north.  The resultant, obtained by the Pythagorean theorem is 728m, and its direction is 15.9º,obtained with trigonometry.

The last type of problem involves vectors which are not at right angles to each other.  Consider this example:

The vector diagram for this problem is shown in Figure 3.2.6. Note that here the second vector is not at right angles to the first so the Pythagorean theorem cannot be used. 

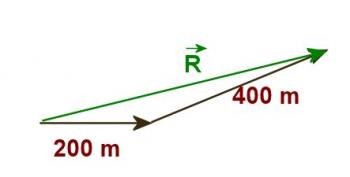
^{Figure 3.2.6}

In this case the second vector is resolved into components as shown in Figure 3.2.7.

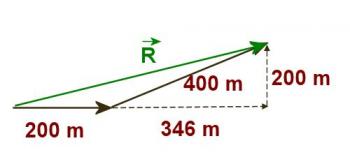
^{Figure 3.2.7}

The east component is 400cos(30) = 346m and the north component is 400sin(30) = 200m.  From here on the problem is exactly like the previous problem since all vectors are either east or north.  The east component of the resultant is 200m + 346m which is 546m.  The north component is 200m.  Therefore, the magnitude of the resultant is 581m and the direction is 20.1ºN of E.

The procedure for adding vectors can be summarized as follows:

1. Select a coordinate axis with the axes perpendicular to each other.  Make use of the geometry of the problem and try to have as many of the vectors parallel to one of the axes as possible.
2. Sketch a neat vector diagram on your set of axes.
3. Resolve any vector which is not parallel to either of the axes into components which are parallel to the two axes.
4. Add the components parallel to one of the axes to find the component of the resultant parallel to that axis.
5. Add the components parallel to the other axis to find the total component parallel to that axis.
6. Calculate the magnitude of the resultant by use of the Pythagorean theorem.
7. Use trig to find the direction of the resultant. 

Subtraction of Vectors

Sometimes it is necessary to subtract vectors.  Although the operation of subtraction is not defined with vectors you can obtain the same result by adding the negative of a vector.  In other words, if you want A - B where A and B are vectors you may compute A + (-B).  The negative of a vector is a vector of the same magnitude as that of the original vector and pointing in the opposite direction.  

1.

Calculate the x‑component and the y‑component of the following forces. Each angle is measured counterclockwise with the x‑axis. 100 N at 30º; 20 lb at 140º; 20 dynes at 260º.

2.

Find the resultant of the following set of vectors: 1.0 lb at 20º, 2.0 lb at 90º, and 3.0 lb at 150º

3.

A man walks 3.0 mi directly northeast, then 2.0 mi east, and finally 1.0 mi southeast. How many miles did he walk?

4.

In the previous problem, specify the x and y coordinates of his final position with respect to the starting point.

5.

In the previous problem, what is his displacement from his starting point?