A vector can be multiplied by another vector or by a scalar.  If it is multiplied by a scalar the product will be a new vector parallel to the first with its magnitude equal to the magnitude of the original vector multiplied by the scalar.

Dot Product

There are two ways of multiplying two vec­tors together.  The first one is called the scalar or dot product.  It is represented by a raised dot between the two vectors as A • B.  The product is a scalar; there is no direction.  The number is determined by multiply­ing the magnitude of one vector by the parallel component of the other.  As shown in Figure 3.3.1 below, that is the same as find­ing the product ABcos(Θ).  However, it is better to remember it as the product of the parallel com­ponents rather than to try to remember this for­mula.

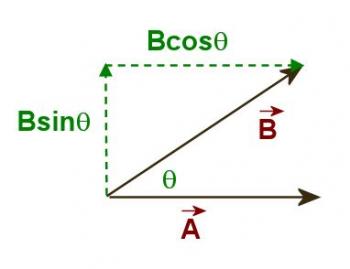
^{Figure 3.3.1}

Cross Product

The second type of vector multiplication produces a vector as its product and is more com­plicated primarily because the direction of the product vector must be found.  This kind of multi­plication is called the vector or cross product and is written A × B.  The magnitude of the resultant vector is equal to the product of one vector and the perpendicular component of the other.  Con­struction of a vector diagram will show that the magnitude of the product is ABsin(Θ), but it is better to remember to multiply perpendicular com­ponents than to remember this formula.  The direc­tion of the product vector will be perpendicular to both of the original vectors.  Careful analysis of the situation will reveal that the two vectors A and B determine a plane and that there two directions the product vector could point and be perpendicular to both vectors.  To find the direction of the product vector it is necessary to use some kind of a mnemonic device. There are a number of these, one of which will be shown here.  Suppose that you are to find the product A × B.  Sketch the two vectors to be multiplied so they originate from the same point as illustrated in Figure 3.3.2.

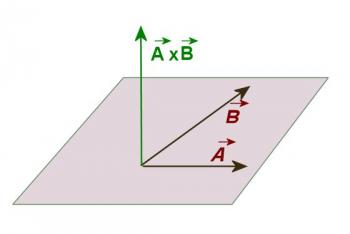
^{Figure 3.3.2}

 Now  imagine a line perpendicular to both A and B intersecting them at the point where they join.  Imagine that you grasp that line with your right hand in such a way that your fingers, which wrap around the line, point from A to B.  Your thumb now points in the direction of the product vector (see Figure 3.3.2).  Note that vector multiplication is not commutative.  If you find the product B × A your fingers must point from B to A  not A to B, and in order to do this your thumb will point in the opposite direction (See Figure 3.3.3).

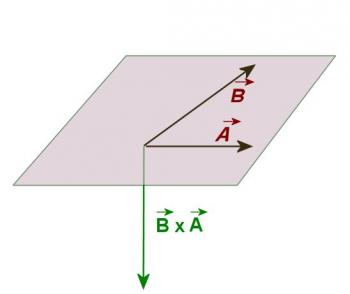
^{Figure 3.3.3}

1.

Vector A is a force of 200N east and vector B is a distance of 40 mi @ 30º N of east. Calculate A × B.

2.

Calculate B × A in the previous problem.

3.

Calculate A • B in the previous problem.