Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Vipin sends us the following question:
_+_+_+80+90=100 , no negetive number in the question.
There are multiple ways to solve this equation, but I have no idea if the ones I came up with are the ones the problem creator was looking for. That's okay. If you come up with a solution that works, it doesn't matter if it's "the right one."
For people reading this question, I'm about to propose a solution, so if you want to try to figure out a solution for yourself, do it now, before you read any further!
--- SOLUTIONS BELOW ---
The first thing I did to this was, I subtracted 80 and 90 from both sides of the equation, which turned it into:
_ + _ + _ = 100 - 80 - 90
_ + _ + _ = -70
If you don't mind, I'm going to replace those blanks with variables, because then I can talk about each individual blank by name:
a + b + c = -70, where a, b, and c are not negative.
I came up with a few possibilities; the first two use complex numbers.
Solution One
a = 0, b = -30 + i, c = -40 - i
I know, you'll be tempted to say, "Wait! -30 and -40 are negative numbers!" To which I reply, "No, -30 is part of the complex number -30 + i. Complex numbers are neither negative nor positive, so I have filled the blanks with numbers which are not negative."
Maybe you'd like to argue that the point is to not use the negative symbol at all. In which case, I give you solution #2:
Solution Two
a = 0, b = 30i2, c = 40i2
I've used no negative symbols, but b and c evaluate to -30 and -40 respectively, giving the desired result.
Maybe you'd like to argue that you can't use negative symbols and you can't use expressions that evaluate to negative numbers. In which case, I would say, "Stop adding to the rules and find your own solution!" ;)
If you're willing to accept solution two, it opens up a boatload of possibilities, like using trig, or other functions:
Trig Solution
a = 0, b = 0, c = 70cos(180º)
If our readers aren't willing to accept any of these answers, please use the "Ask Professor Puzzler" link at the bottom of the page to suggest your own solution. Be sure to mention what blog post you're writing about! If we get any solutions we like, we'll add them to the bottom of the post.
One of my friends shared the following picture on Facebook this morning. He didn't specifically ask me for an answer, but I thought it would be a fun question to explore.

So let's start by asking a question: If it wasn't zero degrees, how would you figure out "twice as cold?" Did you say, "Multiply the temperature by two?"
So, for example, if the temperature was -10 degrees, twice as cold would be -20 degrees?
That seems like it might be a reasonable answer at first glance, except it clearly doesn't work that way, if you just ask this:
If the temperature was 40 degrees, what is twice as cold as that? Now multiply 40 by 2 and you get 80 degrees, which is clearly not colder!
So multiplying the temperature by two doesn't do what we want.
In addition to this, we have another issue with the question: temperature doesn't measure cold. It measures heat. In the same way that we don't measure darkness; we measure light. Amount of light is measured in lumens, and darkness is the absence of light. Cold is not a measured quantity; it is the absence of heat. So saying "twice as cold" may not have any actual meaning to begin with!
The next question to consider is: what scale are you using? Fahrenheit? Celsius? Because that must make a difference too. 0 degrees Celsius is the same as 32 degrees Fahrenheit, and multiplying the first number by 2 gives you zero, while multiplying the second number by 2 gives 64!
Having asked those questions, let's take a break from temperatures and talk about marketing and sales.
I know, I know, that has nothing to do with temperature. Bear with me, though, because I'll get back to temperature in a minute.
Suppose I was hired by a firm to do marketing and sales work. I was hired at the beginning of 2015, and at the end of the year, I wanted to impress my bosses with how much I'd helped the company's bottom line. So I show my boss this chart:
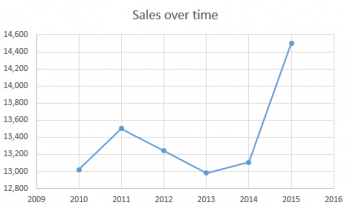
It looks pretty impressive, doesn't it? My boss, if he's not paying attention, will say, "Wow! Look at how much higher the 2015 number is! You've quadrupled our sales, just in one year!"
But if he's paying attention carefully, he'll say, "Wait a minute! Why does your chart's axis start at $12,800 instead of $0?
And the answer is...if my chart started at zero, my bosses wouldn't be nearly as impressed with me:
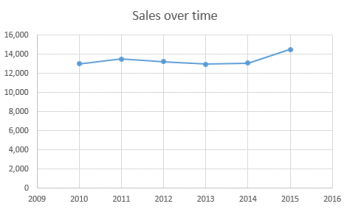
You see, once we have a frame of reference for comparison, we realize that the difference between the 2015 number and the 2014 number isn't nearly as big as it looked in the first chart. And I certainly didn't quadruple their sales, even though it looked like it in the first chart.
The same is true with temperatures: if you want to make comparisons like "twice" or "half," you really need to have a "real" zero. Zero on the Celsius scale doesn't actually "mean" zero, because zero should mean "no heat at all" (just like zero on my sales chart means "no sales at all"). We need to have a scale in which zero really means "no heat whatsoever."
Fortunately, we have a scale like that. It's the Kelvin scale, in which zero is called "absolute zero" because it is the end of the line. There is no heat whatsoever at zero Kelvin. In the Kelvin scale, 0 Kelvin is equal to -273.16 degrees Celsius, and 273.16 Kelvin is equal to 0 degrees Celsius.
Okay, so now let's make some assumptions. Let's suppose that the guy in the picture means 0 degrees Celsius. Let's also suppose that when he says "twice as cold" he really means "half as much heat energy."
If we make those two assumptions, then we can do the following:
0 degrees Celsius = 273.16 Kelvin
Half of 273.16 Kelvin is 136.58 Kelvin
And 136.58 Kelvin is equal to -136.58 degrees Celsius.
There ya go. If the temperature is 0 (assuming Celsius scale), and it's going to be twice as cold tomorrow, it'll be -136.58 degrees Celsius tomorrow. Of course, we had to make some assumptions along the way, but at least we have an answer!
Eighth grader Neha, from New Delhi asks the following question: "I want a set of maths questions of any level with solutions for my holiday homework."
Well, Neha, I'm always happy to see students wanting to do math while on holiday, so I'll make a couple suggestions for you. Of course, I don't know what you've studied, so it's tough to guess what kind of problems you want, but we have a lot of math problems on this site.
You may have noticed our "Pro Problems" section, which is quite large, and getting larger all the time. There are both math and physics problems there, and the math problems cover subjects from basic algebra through pre-calculus topics. Of course, this isn't what you're looking for, because these problems don't have solutions publicly displayed. Those problems are designed for teachers to assign to students, so solutions are only available to teachers.
So instead, if you want to see solutions as well, you can try this page: Maine Association of Math Leagues Problems. These problems were written over the course of several years to help some math competitors get ready for competitions. Some of the problems were written by me, and some of them were written by Sasha, a young man who did exceptionally well in those math competitions.
If you're looking for a harder challenge, you might try Graeme's High School Math Problems, Graeme wrote some very creative and quite challenging problems for this site, over the course of several years.
In these sections, the solutions can be displayed, so you can check your work. Each problem has a clear explanation, not just an answer.
I hope you have fun with your "holiday math!"
Seventh grader omarion, from Georgia, asks, "Why can the “M” and the “D” switch places without changing the order of operations?"
Hi omarion! You've hit on one of the things that is most confusing about Order of Operations. It shouldn't be confusing, but I think sometimes teachers either don't teach Order of Operations correctly, or they teach it correctly but unclearly or incompletely.
You've probably been taught PEMDAS, which stands for: parentheses, exponents, multiplication, division, addition, and subtraction. And you may have been told you can remember PEMDAS by remembering the silly phrase, "Please Exuse My Dear Aunt Sally," in which the first letter of each word corresponds to the first letter of each word in the PEMDAS list.
If that's what you were taught, it's not wrong...exactly...but it's also not complete.
So let me tell it to you a different way.
- Grouping symbols (like parentheses) are most important.
- Exponents are the next most important operation.
- Multiplication and Division are equally important, and they are next after exponents.
- Addition and Subtraction are equally important, and they are after multiplication and division.
- If you have operations that are equally important, you do them in the order that you read the expression (from left to right!)
Multiplication and Division are equally important, so you need to do them from left to right. Similarly, you do addition and subtraction from left to right. So let's try an example problem.
3 · (3 + 5) - 2 ÷ (33 - 52) + 3 · 2
To help you understand how we do this, we're going to simplify it one step at a time. Ready?
Order of operations says that we do parentheses first. But there are two sets of parentheses, right? Which one has higher priority? That's where our last rule comes into play. The one on the left comes first. So first we evaluate the first set of parentheses:
3 · 8 - 2 ÷ (33 - 52) + 3 · 2
Then we evaulate the only other set of parentheses. But wait! the second set of parentheses has multiple operations! Two exponents, and one division! So we tackle this in the following order: first exponent, second exponent, then subtraction. Here it is:
3 · 8 - 2 ÷ (27 - 52) + 3 · 2
3 · 8 - 2 ÷ (27 - 25) + 3 · 2
3 · 8 - 2 ÷ 2 + 3 · 2
So what's next? Multiplication and division. Which is more important? Neither! They're equally important. So we do them from left to right. So follow each step, and see which operation I evaluate in each step.
24 - 2 ÷ 2 + 3 · 2
24 - 1 + 3 · 2
24 - 1 + 6
Now we only have addition and subtraction. Which is more important? Neither! So we go from left to right, which means doing the subtraction, and then the addition:
23 + 6
29
So, in answer to your question, why can we switch the "M" and the "D" in PEMDAS? It's because neither M nor D is more important than the other. Similarly, neither A nor S is more important than the other. So actually, if I wanted, instead of talking about PEMDAS, I suppose I could talk about...
PEDMSA!
Which, of course, stands for...
Professional Educators Delight Many Students of Algebra!
Good morning Puzzling Friends! I have a puzzle for you all.
rinku sends us the following question: "How can we get one using the numbers 1 to 10 in the same order using the four operations?"
This is all we have for details on this puzzle. It is not clear, from the wording, whether parentheses are allowed.
For example, are you allowed to do things like this: 1(2 + 3 - 4) + 5... etc. If you can use parentheses, that simplifies the problem, I'm sure!
I'm curious to see how many different solutions we can come up with. Try doing it without parentheses, and if you can't solve it, try it with parentheses. Use the "Ask Professor Puzzler" link at the bottom of the page to submit your answer.
I'll update this blog post with the first/best submissions, so make sure you check back next week to see what solutions have been shared!
The only solutions which were posted were variations on a single theme.
It occurred to me, as I looked at this, that each pair of successive integers had a difference of one (or negative one, depending on which way you do the subtraction). Thus, if we alternate adding and subtracting differences, we'll get the desired solution:
First we add 2 to -1.
Then we subtract 4 from 3.
Then we add 6 to -5.
Then we subtract 8 from 7.
Finally, we add 10 to -9.
-1 + 2 +3 - 4 - 5 + 6 + 7 - 8 - 9 + 10 = 1
The other solutions received were simply variations on the add and subtract differences concept, such as:
1 - 2 + 3 - 4 - 5 + 6 - 7 + 8 - 9 + 10 = 1.
Many other variations are possible.
Can you find a solution that includes operations besides addition and subtraction? Use the "Ask Professor Puzzler" link to give us your solution!


