Someone told me that "most people have a higher than average number of bones in their body." That doesn't even make sense to me. How can most people be above the average?

Whoever told you that is probably not right, but I'm pretty sure I know what they were reasoning. So first I'll explore their reasoning, and then I'll present an alternate view of the statement.

You see, the 'normal" human has 206 bones in their body, but the average number of bones in the human body, if you were to take a survey of all humans currently alive in the world - is slightly less than 206.

Why? Because some people were born without arms or legs. Others have had limbs amputated. So if you average the number of bones of all the people in the world, you'll end up with a number slightly lower than 206.

Let's just make up some numbers, so you can see what I mean.

We'll say that the population of planet earth is 8 billion people. Of these 8 billion people, we'll hypothesize that 0.5% of them have lost a limb (rough estimate based on the number of people in the U.S.A. with amputations), and that limb loss has cost them 30 bones (I'm completely making that number up).

So we have 7,960,000,000 people with 206 bones, and 40,000,000 people with 176 bones. How many bones is that in total?

7,960,000,000(206) + 40,000,000(176) = 1,646,800,000,000

That's a lot of bones! So to find the average number of bones per person, we divide by our 8 billion figure: 205.85.

Since most people have more than 205.85 bones, most people have a higher than average number of bones in their body.

Okay, so that's the reasoning your friend was using. But it's not quite right. Because, you see, when you are born you have about 300 bones in your body. These bones are connected by cartilage, and will eventually fuse together (the process by which cartilage turns to bone is called "ossification"). How long does it take this process to complete? Well, I don't know for sure. One site I looked at said the process is complete around the age of 20, another said 25. I didn't feel like tracking down more research on that, so let's go with the smaller number, and say the process is done at age 20.

This is important: I'm attempting to prove your friend wrong, which means that at every step, my rounding is going to be done in the direction that favors your friend's hypothesis. Because if he's wrong in the best-case scenario, then we know he's wrong for sure!

Now, I have no idea how many bones a child has at various ages, so here's what I'm going to do. I'm going to assume the best case scenario - every child under the age of 20 has 1 extra bone, leading to a huge chunk of the population having 207 bones instead of 206. Again, I know that I'm lowballing this massively, but my goal is to give your friend's hypothesis the benefit of the doubt.

So now we have to rework our numbers, and for this, I'm going to use 25% as the percentage of people in the world under the age of 20. This number is not completely out of my hat - I based it on some numbers for U.S.A. population, and rounded down a bit. 

In our previous calculations, we had 1,646,800,000,000 bones, but now I want to break it down by adult vs. child, so I'm going to multiply that by 0.75 (75%) to get the number of adult bones:

Adult bones = 1,646,800,000,000(0.75) = 1,235,100,000,000

For children's bones, we'll take the total in our previous calculation and multiply it by 0.25 (25%). However, this number is based on 206 bones per person, so we're going to then divide by 206 and multiply by 207. This number isn't going to come out even, so we'll round down, in fairness to your friend's hypothesis.

Child bones = 1,646,800,000,000(0.25)(207)/206 = 413,700,000,000.

Now let's add the adult bones and child bones together: 1,648,800,000,000. This is only slightly larger than the other number we obtained (because I did so much rounding down), but it's enough to put us on the other side of 206:

1,648,800,000,000/8,000,000,000 = 206.1

So it turns out that most people (the adults without amputated limbs) have a below average number of bones. Bear in mind that some of these numbers I pulled out of a hat without a lot of research, but I think it's safe to say I lowballed enough numbers that we can be reasonably sure of the conclusion. If you disagree, drop me a note with your reasoning!

First of all, I want to make it abundantly clear that this post is not political in nature. It is not an attempt to endorse one candidate, or repudiate another candidate. It is, pure and simple, pointing out how easy it is to misuse mathematics and statistics to try to emphasize a point. Take a look at this image, which is floating around on facebook.

What is the intent of this picture? Well, looking at the caption under the photo, which read, "Who speaks for you? Bernie Sanders 2016," makes it clear that the intent was to show Sanders as a "man of the people" and the rest of them so insanely rich that they are out of touch with the American people.

But the reality is distorted by the image's choice of mathematical language. Specifically, the choice was made to use the text "¾ million" when referring to Cruz's home, instead of the text "750 Thousand." This, I am certain, was deliberate. Because "milllion" sounds massive compared to "thousand," and if they had written "750 Thousand" next to Cruz, people would be much more likely to realize that Cruz is in the same ballpark with Sanders, and not in the same ballpark as Trump, or even Clinton.

To those who are reading quickly, or who didn't do well in math, "¾ million" sounds much larger than "750 thousand," even though the two phrases are expressing exactly the same value.

In mathematical terms, instead of talking about "ballparks" we talk about "orders of magnitude." Two numbers have the same order of magnitude if the larger one divided by the small one is less than 10.

And guess what! Cruz and Sanders have the same order of magnitude. Would you like to see a graph of these values? Here it is:

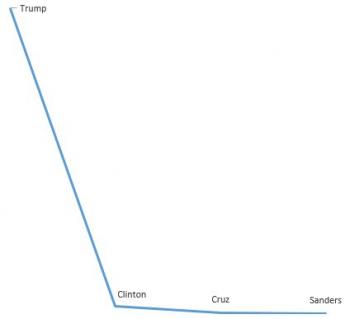
Notice that compared to Trump, Clinton's homes seem inexpensive, but compared to both of them, Cruz and Sanders are downright indistinguishable*.

Do I care how rich these guys are? Not even a whit. I have no problem with a rich president. I have no problem with a middle class president. I have no problem with a poor president.

I have a problem with people using mathematics to deceive the people who do care about such things. A good piece of advice for you when looking at a set of statistics: take note of all the units given (in this case, "millions" was given as the units throughout, until the very end) and if the units are not consistent throughout, ask yourself why. It may be that there's a good reason, but it could very well be (as in this case) that someone is trying to fool you. To keep things consistent, the graphic creator should either have written the Cruz value as "750 Thousand" or the Sanders value as "3/10 Million."

The person responsible for the graphic probably was hoping for one of the following:

1. You slept through the math lessons where your teacher taught you about place value and magnitude.
2. You'll be in such a hurry to click "like" that you won't take a moment to remember the lessons you learned.

After all, it's an election year. What did you expect?

* You might be thinking to yourself, "You really think that the difference between a 300 thousand dollar home and a 750 thousand dollar home is not significant?" And if that's what you're thinking, you're sort of missing the point here. The point is that the person who made the graphic was afraid that if he represented the facts in an honest manner, you would think it was an insignificant difference, and so he chose a dishonest path, hoping that your gullibility would do the rest. 

I was told that the number 1,000,001, no matter what base you're working in, is a composite number. Is this true?

Hmm...that's an interesting question. Let's look at some sample bases to make sure it's a reasonable statement.

If this was base ten, then we'd have 1,000,001 is divisible by 101, so it's composite.

If this was base eleven, then the number would be equal to 1,771,562 (base ten), which is obviously composite, because it's even!

Actually, now that I think about it, any time the base is an odd number, 1,000,001 represents an even number, so it's definitely true for all odd bases. So let's focus on even numbered bases.

Let's try base eight. This number would be equal to 262,145 (base ten), which is a multiple of 5.

Base six? That's 46,657 (base ten), which is divisible by 37.

Now, I could keep trying more bases, but I just noticed something interesting. In our first example, the number is divisible by 101, which is one more than the square of 10, and in our last example, 46,657 is divisible by one more than the square of six. That's interesting. Your number may always be divisible by one more than the square of the base. Let's test that hypothesis.

In base twelve, this number would be 2,985,985, and if our hypothesis is correct, it will be divisible by 12² + 1, or 145. Pull out your calculator...

It is!

So we have a reasonable extension of your conjecture: If 1,000,001 is a number written in base n, then it is divisible by n² + 1.

Ideally, it would be nice if we could prove this extension, because if we could, we'd be closer to proving your conjecture.

Let's write our number 1,000,0001 in terms of the base n:

1,000,0001 = 1·n⁶ + 1.

And suddenly I'm remembering one of my factoring rules - the rule for a sum of cubes:

n⁶ + 1 = (n²)³ + 1³ = (n² + 1)(n⁴ - n² + 1)

Sure enough, 1,000,0001 will always be divisible by one n² + 1!

So in order to finish proving your conjecture, we simply need to show that (n² + 1) can't be equal to 1, and it can't be equal to n. These are the two circumstances which could result in  n⁶ + 1 being prime (a number is composite if it has factor pairs other than one and itself).

n² + 1 = 1 has only one solution: n = 0. But we don't work in base zero, so this is irrelevant.

n² + 1 = n, or n² - n + 1 = 0, which has no real solutions, so YES! The conjecture we started with is true!

Thanks for asking - that was an interesting exercise!
Professor Puzzler

A student asked this question today: "Why is 0! (zero factorial) equal to one, instead of zero?"

Good question! Let's begin by making sure everyone knows what the "!" (factorial) notation means. n! means "the product of all the integers that lie between n and 1, inclusive."

Thus, 4! = 24, because 4! = 4(3)(2)(1) = 24.

6! = 6(5)(4)(3)(2)(1) = 720

The strange thing, though, is that 0! = 1, and that doesn't really seem to match our definition. After all, the integers between 0 and 1 inclusive are 0 and 1, and when you multiply them together, you get zero, not one!

Okay, so maybe our definition is flawed. We'll come back to that later.

The thing is, though, we don't want 0! to be equal to zero, because it's not useful. You see, we use factorials when we're calculating combinations of things, or when we're expanding a binomial to a power.

If you have something like (x + 1)⁵, the n^th term in the expansion of that is (₅C_n-1)x^6-n. That's the binomial theorem.

The problem is, that theorem doesn't work if we say that 0! = 0. Why? Because ₅C₀ = ^5!/_(0!·5!), and if 0! is zero, then we have a division by zero problem! On the other hand, if we say that 0! = 1, then this works out perfectly to ₅C₀ = 1.

And really, if you think about it, that makes sense: If you have five objects, in how many different ways can you choose none of them? Uh, one!

We can see that 0! = 1 makes sense using patterns, too. Consider this:

^7!/_6! = 7
^6!/_5! = 6
^5!/_4! = 5
^4!/_3! = 4
^3!/_2! = 3
^2!/_1! = 2

Now to continue this pattern, what do we need next? 

^1!/_0! = 1

Solve this equation for 0!, and you get: 0! = 1.

Okay, so it makes sense with the combination notation to say 0! = 1, and we can even see from patterns that it must equal 1. So the real problem is our definition. So maybe we should reword our definition a little bit.

I like this way of saying it: For all non-negative n, n! is the product of 1 with all the positive integers less than or equal to n.

Does that work? Sure! It keeps everything else the same, but since there no positive integers less than zero, we're left with 1.

That's one way of getting around it. Another way is to just say For all non-negative n, n! is the product of all the positive integers less than or equal to n. This way of defining it forces us to use the "empty product" definition, which says that multiplying together zero factors gives a result of one.

Or you can define it recursively by saying : 0! = 1, and for all integer n > 0, n! = n(n - 1)!.

Or, you can simply do this: For all positive n, n! is the product of 1 with all the positive integers less than or equal to n, and 0! = 1.

This last one defines n! when n>0, and then gives a special definition for 0!.

No matter how you choose to define it, the real point is that mathematicians chose to define it to be one instead of zero simply because it was of practical use to do so!

Eleventh grade Max from England has a question for us, which references our Vortex Based Math pages:

"Hello prof! Lately I've been finding myself doodling little stars in the margins of my workbooks, seeing what patterns I can make with x number of points in a circle, a rule for arranging lines, making notation for different rules and so on. So far it's just been harmless messing around with patterns, but I saw your post on vortex maths and I'm concerned at the similarities I'm seeing with my own work. I don't think of myself as particularly 'mystic' but I do appreciate the patterns in mathematics, a la ViHart on YouTube and I'd rather not end up like Marko Rodin. My question is, should I keep on doodling and doing pseudo-mathematical patterns or move on and find something else? If so, what related things can I doodle that might bring me a bit closer to actual maths? Thanks for your time"

Well Max, I've got to tell you, this is one of the best questions I've seen in awhile. I like the way you're thinking. Before I answer your question, though I'm going to tell you a little story that your comment about doodling reminded me of.

When I was a kid, maybe in third or fourth grade, while all my classmates were learning addition and subtraction and the like, I was (I confess) a bit bored with math class.

So I started doodling. I doodled a tiny five-pointed star in the middle of my note paper. Then I drew a pentagon around it. Then I drew another star outside of that, and then another pentagon, and then another star, until my entire page was filled with stars within stars within stars.

And then I realized there was someone standing over my shoulder watching what I was doing.

It wasn't my teacher. Oh no, it was worse than that. It was the District Mathematics Curriculum Coordinator. And when you've been caught doodling by someone with such an impressive sounding title, it's a bit terrifying.

But Mr. Tame just asked me quietly, "What have you learned?"

I was a bit flustered (to say the least) but I had enough presence of mind to stumble out a response about how my first star wasn't perfectly drawn, and the more stars I drew, the more those errors got magnified.

He nodded thoughtfully and said, "That's a pretty important lesson," and then moved to look over the next student's shoulder.

I breathed a big sigh of relief and turned my attention back to addition and subtraction.

I appreciated Mr. Tame's willingness to let me get away with doodling. Because I did figure out something important about error and percent error (which I certainly could not have put into words at the time, but as Mr. Tame said, it was an important lesson).

So don't be afraid to doodle. Don't be afraid to explore. Don't be afraid of patterns. But don't stop just because you've found your pattern. Now ask the question, "Why?"  That's where Marko and his buddies fell apart. They thought the pattern was the end of the quest. But the pattern was just the beginning. From there they should have gone on to ask questions like, "What is the cause of these patterns?"

I love that you referenced ViHart. Have you watched her video about the golden ratio and Fibonacci numbers? If you haven't you should. There are some amazing, astounding patterns related to the Fibonacci sequence and the golden ratio that show up in nature. But ViHart doesn't just say, "Have you noticed that the leaves of a plant spiral in patterns related to Fibonacci numbers?" She says, "These are astounding patterns, and let's see if we can figure out why a plant's leaves tend to grow in this way!"

That's the difference between a Rodin and a ViHart. One is satisfied to find a pattern, the other wants to know why the pattern exists. Some of the most interesting mathematics and science stems from people discovering patterns and then trying to figure out why they happen.

A wise old king (Solomon) once said, "It is the glory of God to conceal a thing: but the honour of kings is to search out a matter." The universe is filled with extraordinary and beautiful patterns. They're like a buried treasure hidden just below the surface. But don't just find them. Dig them up. Search them out. Understand them.

And if you can't answer the question "Why?" Don't get discouraged. Go find something else to explore, and maybe someday down the road your explorations will connect some dots, and you'll have an answer to the question that you couldn't answer today!

Thanks for writing, Max!

Professor Puzzler