The question of the day is: 

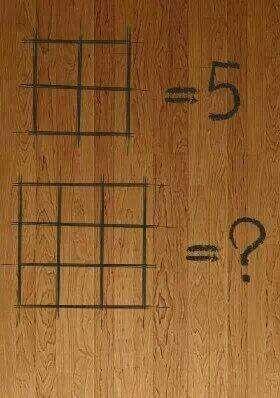
Can you solve it? If you said "yes," Then you are probably wrong. This is really not a "solvable" problem. It was created by someone who wanted to generate arguments and disagreements, because arguments translate into attention, likes, and shares.

You see, it's pretty much impossible to draw conclusions about a pattern when you only have one example from which to draw your conclusions. Depending on what pattern you notice, there are a multitude of "correct" answers.

I think the most common conclusion is: 5 is the number of squares in the image (four little ones and one big one). If this was your interpretation, then the answer is 14 (9 little squares, four medium squares, one large square).

However, there are other ways of interpreting the image. 5 is the number of line intersections involving interior line segments. In which case, the number for the second image is 12.

Another way of looking at it: 5 is the number of squares which border on the edge of the diagram. In which case, the answer to the second diagram is 13 instead of 14, because one of the squares (the central little square) doesn't border on the edge of the diagram.

But we don't have to stop there - as Brian Twitchell (District Math Coach, RSU #74) points out, we can create even more patterns:

• If we take one less than the number of horizontal unit segments, we end up with an answer of 11.
• If we take seven less than the sum of the number of horizontal and vertical unit segments, we get an answer of 17.
• Forget unit segments; consider line segments that span the length/height of the diagram. Now subtract one. This also matches the original diagram, and gives an answer of 7.

 So don't be too quick to assume you have "the" answer to a question!

If you enjoyed this post, you might also be interested in Professor Puzzler's analysis of this sneaky problem:

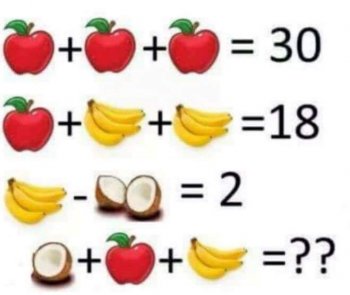
The image below has been showing up in various incarnations on the internet. Sometimes with an image of Albert Einstein, sometimes with an image of Sheldon from "Big Bang Theory."

I especially find this meme ridiculous when it's accompanied by a picture of Sheldon posing this as a problem for Penny, because anyone who knows Sheldon, and knows anything about math, know perfectly well that Sheldon would never, ever, ever pose a problem like this. Instead, he would, like good ol' Albert in the image below, give it an emphatic thumbs down.

What would Sheldon say the answer is?

He would say, "Three. The answer is three. Bazinga!"

Einstein probably wouldn't say "Bazinga," but he would agree. The answer is three.

"But," someone might protest to Sheldon, "That doesn't fit the pattern!"

"Oh," Sheldon would say, "You want a pattern? Okay. The answer is the square root of seventeen."

"No," you would say, "That's wrong."

"Exactly," Sheldon would say. "You wanted me to create a pattern. The first four equations are wrong, so I made another wrong equation to complete the pattern. Bazinga again!"

Einstein would probably answer differently. He would probably say, "Just because the first four equations are wrong doesn't mean I have to be wrong, too. The answer is three."

You see, in mathematics, the equals sign has a very specific meaning; it means that the two sides of the equation are equal. So I don't care if the person who made this meme got four equations wrong, the answer is still three.

What the problem writer probably meant to do was to use function notation:

f(8) = 56
f(7) = 42
f(6) = 30
f(5) = 20
f(3) = ?

Now we at least have valid mathematical notation. But is the problem solvable? Not really, no. Because there isn't just one function which satisfies the values above, and not all of them produce the same value for f(3).

For example, the function that the image creator probably wanted you to use was: f(x) = x² - x, which works for all the values given, and gives f(3) = 3² - 3 = 6. This is the answer most people are accepting as correct. However, consider the following as an alternative function:

f(x) = (x³ - 4x² + 3x)/(x - 3)

With this function, we get the correct values but we can't plug three into the function because it results in a divsion by zero!

So, even if we fix the notation, the real geniuses will tell you that it can't be solved.

Bazinga.

Addendums

• Phil wanted to know if I could find a function that matched all the data points in the pattern. but produced a different value for f(3). (Apparently he thought it was cheating to create a function that has no value for f(3)!). Anyway, the answer is, yes, I can do it, and here's the explanation of how: Creating Einstein's Meme Function.
• Toward the end here I'm being a bit tongue in cheek, pointing out that there isn't just one solution. For most of us, though, if we can find a pattern that matches four data points, we feel like we've come up with a satisfactory "solution."  It's a whole different matter if you're given only one data point and asked to find a pattern, which is what happens in the puzzle linked below. Be sure to read about the "squares" problem for more about that!

Click the image below for another question and answer!

Seventh grader Colton from Florida asks, "If triangles have the same area, are they similar? Or do triangles have to have the same perimeter to be the same? I think it's area. Thank you "

Hi Colton! 

Thanks for your question. I want to make sure we're talking about the same thing here. In one question you talk about triangles being "similar" and in the next you talk about them being "the same." These are two very different questions, that use very different concepts.

You see, triangles could be congruent (what you might have meant when you said "the same") or they can be similar.

So what is the difference?

Congruent means that two triangles are identically shaped. The have the same shape and the same size.  They have three pairs of sides that are the same length, and they have three pairs of angles that are the same measure. We call the pairs of parts "corresponding parts," and we say that in congruent triangles, "Corresponding parts of congruent triangles are congruent" (which gets shortened, often, to "CPCTC").

Another way of saying that: if you have two triangles that are congruent, you could pick one of them up and set it down on top of the other, and they would match perfectly. You might have to flip or rotate the one you picked up, but if you can't make it line up perfectly on the other triangle, they aren't congruent. In the image below, the triangles are congruent, because you could pick up the one on the right, rotate it about 45 degrees counter clockwise, and it would fit exactly on top of the triangle on the right.

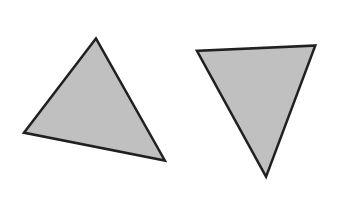
As for your question: if two triangles have the same area, are they congruent? Not necessarily! I can create two triangles that take up the same amount of space, but have very different shapes. And the same is true of perimeter; just because two triangles have the same perimeter, that doesn't mean they're the same shape.

There are ways to tell if two triangles are congruent. For example, if you have two pairs of sides that are the same length, and the pair of angles between those sides is congruent, then it's guaranteed that the two triangles are congruent. Maybe in another blog post I'll explore all the different congruence theorems!

But now we need to consider similarity. Similarity is different from congruence. Two triangles can be similar without being congruent. Two triangles are similar if they have the same shape, but not necessarily the same size. What do I mean by "same shape?" Well, one way of explaining it is to say that all of their pairs of angles are congruent. 

Or, imagine that you have two similar triangles printed on transparencies. You might not be able to lay one on top of the other so that they match, but if you hung one of them on the wall, and used a projector to project the other one onto the wall, you could make them line up by getting the projector the right distance from the wall.

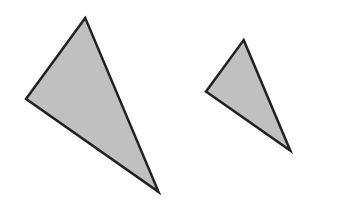
This picture is an example of two triangles that are similar. You can see the shape is the same; they both have two smallish angles, and one bigger angle. You couldn't lay one of them on top of the other and have them match perfectly, but if you expanded the smaller one, you could make it fit perfectly on the larger one. They are similar.

Okay, so now we come back to your question: if two triangles have the same area, or the same perimeter, are they similar? Not necessarily! You could have two triangles with the same perimeter (or the same area) that aren't the same shape at all. And if they're not the same shape, they're not similar!

So, in conclusion, neither the area nor the perimeter will help you determine if two triangles are similar, or determine if they are congruent!

That's a pretty long answer to a short question, but hopefully you learned some important concepts along the way.

Thanks for asking your question, Colton.

Sincerely,
Professor Puzzler

I don't normally do follow-up posts on subjects I've already written up, because most of the time when I get e-mailed questions or comments about things I've written, I feel like they are best suited to a discussion in our community forum, rather than creating extra blog posts. However, this particular question, even though it is a follow-up to the Apples, Bananas, and Coconuts blog post, is worth analyzing in its own right, independent of the previous blog post.

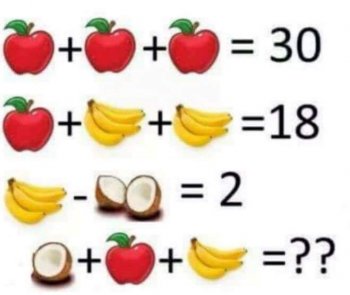
In the image shown here, the challenge was to find the value of an apple, three bananas, and half a coconut. There are multiple ways of assigning meaning to the images. For example, your basic banana "unit" could be 1 banana, or it could be 1 banana bunch (in which case, the last line contains 3/4 bunch!).

Similarly, your basic coconut unit could be a coconut, or a half-coconut. How you define these will affect how you work out the problem, but does not affect the solution.

One reader was concerned by the fact that you can end up with two variables having the same value: a half-coconut has the same value as a banana, and "this is not algebraically correct, as in algebra, X & Y cannot both be equal to one."

And this is the question we're exploring here: Can two variables have the same value in a problem?

The question-writer is not the only one who gets flustered by this possibility -- I have algebra students who get flummoxed every time I give them a problem in which both X and Y have the same value; they are convinced they must have done something wrong! In fact, just last week I gave my algebra students a system of three equations in three unknowns, in which the variables x, y, and z all were equal to one.

Really, there is no algebraic reason why two variables can't have the same value.

First, let me give you a graphical representation of an equation. Consider the following equation: y = 4 - x. If you graph it, it looks like this: 

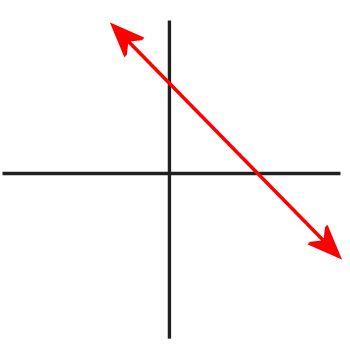
But what does that graph mean? It is simply a graphical representation of every ordered pair (x,y) that satisfies the equation. The red line is an infinite series of x and y values that make the equation true. But did you realize that there's a point in that graph for which x and y have the same value? It's true! It's the point x = 2, y = 2, because 2 = 4 - 2. If having two variables with the same value was illegal, then your algebra teacher would have taught you to graph the equation like this instead, leaving out the point (2,2):

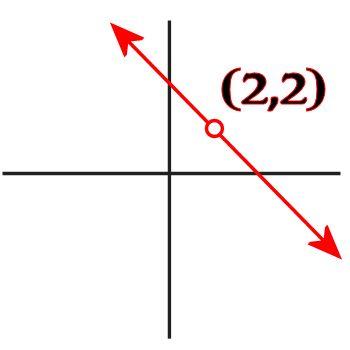
But your teacher didn't tell you to graph lines like this. Why? Because it's perfectly okay for two variables to have the same value!

There are practical implications that would result from supposing that x and y can't have the same value, because algebra was designed to have real-world application. Imagine an accident reconstruction expert is trying to figure out what happened when two vehicles collided. He sets up equations, assigning variables to all his unknowns, plugs in the values he does know, and then calculates the values of his uknowns.

Then, when he gets to the end of his calculations, he says, "Wait! This accident can't possibly have happened! Because the initial speed of the first car was 45 mph, and the initial speed of the second car was also 45 mph! We can't have the same value for two variables!"

No, of course he doesn't say that! In fact, if the speed limit was 45 mph, he'll just smile and say, "At least they were both going the speed limit!"

Or suppose you go shopping, and you pick up a bag of apples and a bag of pears. The bag of apples has 20 apples, and costs $4.00. The bag of pears has 10 pears, and costs $2.00. You think, "I wonder what is the cost of a single apple, and the cost of a single pear?" So you do set up two equations: 20a = 4 and 10p = 2, and to your horror, find that both apples and pears cost the same per fruit "That can't be right," you say, as you hurriedly put the fruit back on the shelf, "I had two variables, and they both came out to the same value!"

Of course not! You'll buy the apples and the oranges at the same unit price, and the universe won't explode! Because, you see, the real world doesn't really care about whether two quantities are equal or not. The values are what they are, and life goes on.

Someday I'm going to write a system of 26 equations in 26 unknowns, in which all 26 variables have the same value. My students' brains might explode, but nothing else will!

Historical note on this blog post: This question was originally asked and answered in 2005 - more than a decade ago! It became one of the most popular pages on the "Ask Doug" blog, and began circulating widely on the internet. As it went along, portions of it were modified, garbled, or even deleted, until eventually it came to the attention of those kind folks at Snopes, who wrote an article about this article, verifying the information within it. Imagine my surprise when one day my wife received her weekly Snopes e-newsletter, and at the top of the e-mail was my blog post!

The blog post has been moved to the "Ask Professor Puzzler" blog as part of our process of consolidation.

Question: I got an email from my * company, and it talked about logging in at their 'secure site', and it mentioned https and http. What is that?

Answer: HTTP stands for HyperText Transport Protocol, which is just a fancy way of saying it's a protocol (a language, in a manner of speaking) for information to be passed back and forth between web servers and clients. You really don't need to know what it all stands for; the important thing is the letter S which makes the difference between HTTP and HTTPS.

The S (big surprise) stands for "Secure". You probably didn't need me to tell you that, because you already knew it had something to do with security. If you visit a website or webpage, and look at the address in the web browser, it will likely begin with the following: http://. This means that the website is talking to your browser using the regular 'unsecure' language. In other words, it is possible for someone to "eavesdrop" on your computer's conversation with the website. If you fill out a form on the website, someone might see the information you send to that site.

This is why you never ever ever enter your credit card number in an http website!

 But if the web address begins with https://, that basically means your computer is talking to the website in a secure code that no one can eavesdrop on. You understand why this is so important, right? If a website ever asks you to enter your credit card information, you should automatically look to see if the web address begins with https://.

If it doesn't, there's no way you're going to enter sensitive information like a credit card number!

It should be pointed out that just because a website has that magic "S" in its address, that does not mean it is wise to do business with them; even scam artists can have https sites!  It simply means that no outsiders can eavesdrop on your conversation...doesn't mean you should be having the conversation in the first place.  Only do business with reputable firms, or firms you have thoroughly checked out!