Today's post is about a picture that has been mystifying and frustrating people. Frustrating because it seems so blatantly and completely wrong. Mystifying because people in the know just smile knowingly as though it's a joke.

Some jokes need to be explained, so here's the picture:

It seems quite clear, doesn't it? PEMDAS gives us our order of operations. We evaluated 85 + 65 first: 85 + 65 = 150.

So now we have 25 - 55 + 150, which should be evaluated in order from left to right: 25 - 55 = -30, and -30 + 150 = 120.

So how in the world did they get 5?

The answer is: they didn't get 5. They got 5!

You see, this is one of those horrible times when mathematics hijacks innocent punctuation marks and forces them into hard labor for nefarious, non-grammatical purposes.

The exclamation mark is used in mathematics not to epxress excitement or astonishment, but to indicate that we are calculating the factorial of a number.

What's a factorial? A factorial is what you get when you multiply all the integers between 1 and some number. For example, 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720.

So before we declare this image bogus and invalid, we probably should check to find out what 5! equals.

5! = 5 x 4 x 3 x 2 x 1 = 120.

Oh! (And I'm using that exclamation mark to indicate astonishment) it really does equal 5!

And if I'm truly astonished, I might say that it equals 5!!

Except someone might get hoodwinked into thinking I meant 120!, which is about 6.8 x 10¹⁹⁸. That's not what I meant. I promise. I'm just that excited!

What is the solution to the following puzzle that's been going around facebook?

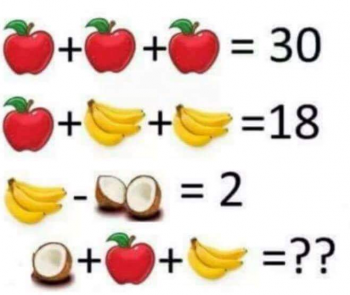
The answer is, on the surface, not terribly difficult to find:

3 apples = 30, so 1 apple = 10.

10 + 2 bananas = 18, so 2 bananas = 8 and 1 banana = 4

4 - 1 coconut = 2, so 1 coconut = 2

Therefore, 1 coconut + 1 apple + 1 banana = 2 + 10 + 4 = 16

HOWEVER...

Although this is the answer everyone seems to be giving, it's actually not correct. Notice that each bunch of bananas has four bananas (look closely!) except the one in the final line, which has 3 bananas. Also notice that the third line has one coconut, while the last line has only 1/2 of a coconut. 

This changes things!

3 apples = 30, so 1 apple = 10.

10 + 8 bananas = 18, so 8 bananas = 8 and 1 banana = 1

4 - 1 coconut = 2, so 1 coconut = 2

Therefore, 1/2 coconut + 1 apple + 3 bananas = 1 + 10 + 3 = 14

This is a really nice problem, since it gives you a good reminder to pay attention to details!

Click the image below to read Professor Puzzler's analysis of another puzzle:

Addendums

William from Phoenix asks, "Apples coconuts bananas: The editing to remove the fourth banana was incomplete. it left the end point in the picture on line four. Was that intentional to cause controversy with your answers?"

Honestly, William, I can't see the incomplete erasure you're talking about. I don't doubt you, but I'm not seeing it. But, since you asked, I'll take this opportunity to point out: I didn't create this problem; I just wrote up the solution for people who wanted to know. If I had to make a guess, I would say that the person who created it did not intentionally leave part of a banana; they probably were just inexperienced with photoshop, or were in a hurry when they created it! 

Colton from Florida had a question about the Algebra of this problem, which we answered here: Can X and Y have the same value?

Pany from UK points out that there is another way to interpret the problem, in which we regard each image as a symbolic variable, rather than as collections of real world objects. While I don't agree with him that this is the best way of looking at it, it is absolutely a valid way of viewing the problem, and it results in a very different problem, which is unsolvable, because we have more variables than equations. And speaking of which...

Anne from Maine shared with us a similar looking problem with a very different solution. Click the image below to read that post:

"Where does the apostrophe go in Presidents Day? Is it before the 's,' after the 's,' or nowhere?"

This is a fun question to look at for the month of February. In a couple weeks students across the country will be on vacation for a week, and their vacation will begin with the federal holiday called...

Presidents Day?
President's Day?
Presidents' Day?

Which is it? The surprising answer is: None of the above!

That's right - there is no federal holiday named any of those variations on "Presidents Day." The actual federal holiday is named "Washington's Birthday," with the apostrophe before the 's,' because we're only celebrating one Washington. If we were celebrating George Washington and George Washington Carver, we would call it "Washingtons' Birthdays" or something like that.

But if the holiday is officially known as "Washington's Birthday," why do we call it "Presidents Day"?

The answer to that stems from the fact that Lincoln's birthday is near Washington's birthday, and there was a push to make the holiday a celebration of both birthdays. And there was also a push to make it a celebration of all presidents.

Who made this push? Various states. You see, even though the holiday is officially called "Washington's Birthday" by the federal government, many states have implemented their own names for the holiday.

Which brings us back to the original question, with the qualification that now we're talking about state holidays. And the answer is: ALL THREE.

That's right; since each state gets to implement their own state holidays, and none of them agree, exactly, on how to implement it, the holiday gets named differently depending on how the state intends it to be celebrated.

For example, if you live in New Jersey (and a few other states), you celebrate the day without any apostrophes. Congratulations, New Jersians - you don't have to worry about where that apostrophe belongs!

If you live in Texas, you are celebrating multiple presidents, so you celebrate "Presidents' Day."

If you live in Maine, you are either celebrating a single president (presumably Washington) or you are celebrating the office of president, because you celebrate the singular "President's Day."

Some states choose not to use the word "President" at all, calling the holiday things like "Washington's Birthday" or "Lincoln's Birthday" or the somewhat convoluted title "Washington's and Lincoln's Birthday." 

Montana seems to prefer Lincoln over Washington, since they reverse it to "Lincoln's and Washington's Birthday"

Interestingly, a couple southern states eliminate Lincoln altogether from the holiday; Alabama replaces him with Thomas Jefferson, and Arkansas replaces him with civil rights activist Daisy Bates.

Did your state not get mentioned in this post? Head on over to Wikipedia and search for "Washington's Birthday" and you'll get a more detailed analysis.

And enjoy your holiday, whatever you might call it!
Professor Puzzler

We've had several questions recently about how to find terms of a geometric sequence, if you've been given specific information about the sequence, such as, what two of the terms are.

So let's consider a couple examples. For starters, let's say we have a sequence in which the second term is 4, and the fifth term is 27/2. How do we find the first term and the common ratio?

First, since the n^th term is ar^n-1, we know that ar = 4, and ar⁴ = 27/2. So what do we do with these two pieces of information? Well, we can take the second equation and divide it by the first one, to obtain r³ = 27/8, or r = 3/2.

Since we know that r = 3/2, we can plug that into our first equation, and get (3/2)a = 4, so a = 8/3.

Not too bad, right?

So let's try another one that works out to be just a little different.

If the second term is 24, and the fourth term is 6, find the first term and the common ratio.

We start out the same way:

ar = 24, and ar² = 6. Dividing these two equations gives r² = 1/4.

At this point, it's tempting to take the square root of both sides and say r = 1/2. (I see algebra students do this all too often!)

However, it's important to remember that 1/4 has TWO square roots: 1/2 and -1/2.

This means there are TWO possibilities for a. If r = 1/2, then a = 48, but if r = -1/2, then a = -48.

As a general rule of thumb, if you're given two terms of the same parity (both odd numbered terms, or both even numbered terms) you're going to have two possible solutions.

Thanks for asking, and good luck with your sequences!
Professor Puzzler

This site has an extensive reference unit on the topic of Codes and Secret Messages, and because of that, people often make the assumption that I want to help them decode their own personal secret messages. This is actually rarely the case. Actually, I think in decade plus that this site has been online, there's only been one instance where I helped someone decode a secret message. It was a Harry Potter code, and I turned it into one of the "Easter Egg" pages on the site (good luck finding it!).

I've even put a notice on the "Ask Professor Puzzler" contact page, letting people know that I'm not in the business of translating their secret messages for them. But the codes keep coming.

So we've added a new section to the community forum called "Codes and Secret Messages". This is a place where - if you are a member - you can post a code, and ask the community for help decoding it. Please note that in order to post a message in the forum, you must be a member, AND you must have played (and completed) at least five games on this site (that's our own version of a CAPTCHA - instead of asking you to read a convoluted, messy line of text, we ask you to solve puzzles; it's much more in keeping with the nature of the site!).

So if you've got a message, a code, or a riddle that needs decoding, head on over and ask for help!