Pages from this blog, our reference pages and lesson plan pages, and other informational pages on the site have been cited in a variety of forms, from wikipedia pages to scholarly dissertations. Most people aren't thinking about formal citations - they just want to link to our pages (and we welcome that), but we do occasionally get requests for the proper way to attribute information quoted on this site. Here is the proper citation method.

If the publication date and author of the page are displayed on the page, you will cite the page like this:

{Author's name} ({date}). {Page title} [{content type}]. Retrieved from {URL}.

For example, if you wanted to cite the post on this blog about the force of gravity in a spherical shell, it would look like this:

Note that all blog posts on the "Ask Professor Puzzler" blog have the same author. You can find the date the article was posted under the article title. Also note, that for online citations, URLs should be in the form of a clickable link to the page you found the content.

Many pages, do not have a publication date. If that's the case, you can simply skip that item:

{Author's name}. {Page title} [{content type}]. Retrieved from {URL}.

And, most common of all, there is neither an author nor a publication date. Many of the lesson plans and reference units posted on this site were written by teachers and other educators who provided us only an e-mail address and/or screen name. In this case, you begin with the title.

If you want to cite something on this site, you don't need to ask permission first. However, we'd love to know about how our content is being referenced, so we'd be glad to hear from you about it, if you wanted to drop us a note. You may use the Ask Professor Puzzler form to do so.

Judah asks a fairly lengthy question about musical instruments. In a nutshell, he's trying to understand the mathematics behind why musical instruments are not "perfect." His example uses stringed instruments like guitars and ukeleles. He comments that even on the best guitars, if the strings are perfectly in tune, pressing down the finger for a note higher up will never be "perfectly" in tune. He wonders why musical instruments can't be made "perfect." 

For starters, Judah, we should begin by noting that there really is no such thing as "perfect" - when the luthier puts the fret in place on the neck, how close to exact does he have to be for you to call it "perfect?" To the nearest 0.1 cm? To the nearest 0.01 cm? To the nearest 0.00001 cm? To the nearest molecular width? We should probably make our own definition of "perfect" - for our purposes we'll say a musical instrument is "perfect" if the difference between the actual note and the "perfect" note is not distinguishable to our ears. Perfection, then, will vary from one person to another. For example, I have a much better sense of pitch than most of my music students; they can play notes that they think are in tune, but I can tell that they're not. As you increase in musical ability, "perfect" (by our definition) becomes a bit of a sliding scale.

For our discussion here, let's say that being off by less than 0.1% is "perfect". This would mean that if you hear a note that is 439.5 hz, you can tell that it's not 440 hz.

You mentioned ukeleles and guitars, saying that ukeleles are more likely to have intonation problems, and here's the math behind that: the frequency of the note played is inversely proportional to the length of the string (the longer the string, the lower the frequency of the note). On a ukelele, that length is 33 cm, and on a guitar it's 63 cm. Let's say that a luthier can place a fret to within 0.05 cm of the proper position. On a guitar, that's 0.05 / 63 * 100 =  0.07% error based on the full length of the string. On the other hand, for a ukelele, that's 0.05 / 33 * 100 = 0.15%, which is roughly twice the percent error. This difference highlights the fact that it's possible for a luthier to make good guitars, but not be talented enough (or have good enough tools) to make ukeleles; he would need to have better tools, better precision, to make a satisfactory ukelele.

In theory, then, the larger the instrument, the easier it is to make it "perfect." But your question goes beyond what a luthier can do - you're saying that even if the luthier's work is "perfect', the guitar still isn't "perfect." Okay, so let's dive into some of the math more deeply. There's a formula (I had to look this one up - it's not one I remember off the top of my head!) for the frequency of a string:

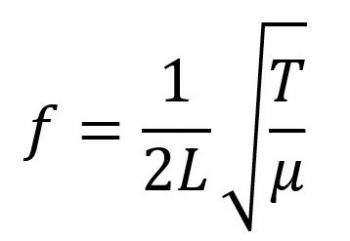
The important things for us to consider here are the L and the T. L is the length of the string (hence, the inverse proportion, because that is in the denominator) and T, which is the tension in the string. Note that the frequency is directly proportional to the square root of the tension.

You can easily see that this makes sense; when you tighten the pegs on your guitar, you are increasing the tension, and the frequency goes up. Similarly, when you put your finger down on the frets, you decrease the length, and in so doing, you increase the frequency.

So with this in mind, let's take a look at my guitar.

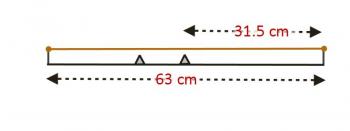
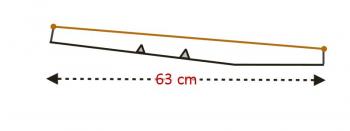
Here you can see the length from nut to bridge, with a couple frets shown, and the string above them. On my guitar, the length from nut to bridge is 63 cm. The vertical distance from the top of a fret to the string is 0.2 cm. Since the frequency is inversely proportional to the length, it stands to reason that if we have a fret halfway between nut and bridge, that'll be an octave (twice the frequency). So I've shown that fret. But wait...what happens when you press down? You now have this situation:

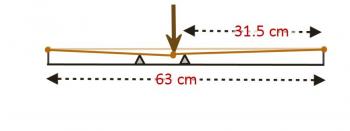
You've put your finger down behind the octave fret and pressed. In so doing, you did two things. First, you increased the tension in the string (thereby making the note sharper), but at the same time, you've also increased the length of the string being plucked (to see why, consider the right triangle shown below.

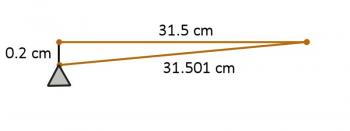
You've increased the tension (raising the note) and increased the length (lowering the note). Thankfully, these two changes are in opposite directions, so they help to cancel each other, rather than adding together. However, this means that a perfectly centered fret may not produce the note you want. Luthiers may use this information to compensate - on my guitar, the octave fret appears to be a very small fraction of a centimeter off-center. So even this issue can be resolved. Except...what if your finger is pressed closer to the fret behind the octave fret? Doesn't that change the tension, without changing the length?

But none of that is the big issue. That was just to get you thinking about the geometry of tension and length. The big issue is that we tend to think of musical instruments as static objects, when in fact they are not. Guitars, ukeleles, violins, cellos, etc are made of wood, and wood is a non-uniform, unpredictable substance. The moment the guitar leaves the luthier, it begins a lifetime of heat and cold, humidity and dryness, high pressure and low pressure, and all of these things affect the shape of the guitar. Anything that affects the shape will affect the intonation.

If the luthier doesn't pick excellent wood, it is prone to warping.  This tendency to warp is why (in construction) it is better to screw two 2x4s together instead of using a single 4x4; the two 2x4s are not likely to warp in the same direction, which means each 2x4 helps to prevent the other from warping, and you're more likely to get an unwarped structure.

Even if the very best quality of wood is chosen, humidity changes the shape of the guitar. This is why your guitar has a rod going down the neck, and an allen nut that lets you adjust the angle of the neck. Look at it this way: in the winter time (low humidity) you may be more likely to get fret buzz, because the strings are closer to the neck, and in the summer (high humidity) you might need to press harder on the strings, because the strings are further from the neck. Let's take that last idea, and really exaggerate it in a diagram:

What does this do? The big thing is that it makes you press harder to get the string down, which significantly increases the tension in the string. BUT, the closer to the nut you get, the closer to the frets the string is, which means there's less pressure required, and the strings are less out of tune. So if you play an instrument and realize that the further up the fretboard you go, the more out of tune the guitar is, odds are good that neck needs to be adjusted.

There are undoubtedly many other things that come into play; I'm not an expert on the construction of musical instruments. But this will hopefully give you a good sense for some of the challenges in building - and maintaining - musical instruments.

One of the interesting things about all of this is that - as you mentioned - it's not necessarily a bad thing to have "imperfect" instruments. One of my favorite sounds in an orchestra is the violin section playing in unison way up high. It produces an ethereal sound, which can be directly attributed to the fact that none of the violinists are playing exactly the same frequency. That "cloud" of frequencies centered around the "right" frequency makes a wonderful sound. In fact, it's so wonderful that effect machines are designed to reproduce it - it's called a "chorus effect." A chorus effect creates multiple copies of the actual sound of a voice or instrument and shifts it slightly in time and in frequency to produce that almost-unison sound that is so wonderful to hear.

Chanchal from Muktsar asks if we could prove that in a quadrilateral the sum of exterior angles is 360°.

Good morning, Chanchal. One of the challenges of doing proofs on this blog is, a proof is constructed from the building blocks of things we already know, stacked together to create something we don't already know, and since I don't know you, I don't know what building blocks (knowledge) you have that you can build from. So before I start talking through the proof, here are some of the building blocks I'm going to use - in case you don't already know these things:

• the sum of the interior angles in a triangle is 180°
• when two lines intersect, they form four angles that add to 360°.
• vertical angles are congruent (vertical angles are the angles across from each other formed by two intersecting lines)

Okay, with that as background, let's look at a diagram.

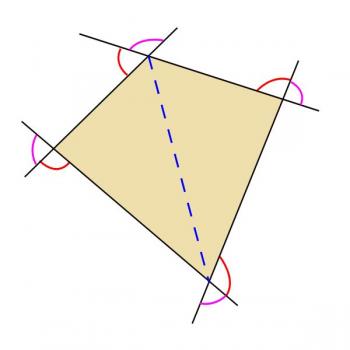
Now, my diagram is not just a quadrilateral - I've added some extra lines into it.

• The blue dashed line is a diagonal of the quadrilateral
• The sides of the quadrilateral have been extended to form exterior angles
• The purple arcs indicate angles which are opposite (vertical) to the interior angles of the quadrilateral
• The red arcs indicate the angles we're interested in.

Note that when we talk about the exterior angles of a quadrilateral, we're not talking about all the angles formed by the sides that lie outside the quadrilateral. We're not including the purple angles, and we're also not including the angles opposite the red ones. The exterior angles are all the angles "facing the same way" around the quadrilateral. That's not a very precise way of describing them, but hopefully you can see from my picture what I mean by that.

Okay, so how do we prove this? I'll give you two methods, and you can decide which one you like best. Ready?

Proof #1

• A quadrilateral can be divided into two triangles by a diagonal
• Each triangle has 180 degrees
• 180 x 2 = 360, so there are 360 degrees in the interior of a quadrilateral.
• Call these four angles a, b, c, and d. Then a + b + c + d = 360
• Each angle is supplementary to an exterior angle.
• Thus, the exterior angle measures are 180 - a, 180 - b, 180 - c, and 180 - d
• Adding these together gives (180 - a) + (180 - b) + (180 - c) + (180 - d) = 720 - (a + b + c + d)
• Since a + b + c + d = 360, this is equal to 720 - 360, which equals 360 degrees.

Proof #2

(Proof #2 starts out with some of the same steps as Proof #1)

• A quadrilateral can be divided into two triangles by a diagonal
• Each triangle has 180 degrees
• 180 x 2 = 360, so there are 360 degrees in the interior of a quadrilateral.
• Call these four angles a, b, c, and d. Then a + b + c + d = 360
• The intersecting lines at the four vertices form angles adding to 360 degrees
• Since there are four such sets of angles, their measures add to 360 x 4 = 1440 degrees.
• The purple angles from vertical pairs with the interior angles, so their measures are a, b, c, and d
• Thus, the sum of the red angles and their vertical counterparts is 1440 - (a + b + c + d) - (a + b + c + d) = 720 degrees
• Since vertical angles are congruent, we divide this sum in half to obtain the sum of the red angles: 720 / 2 = 360 degrees.

Incidentally, this proof can be extended to show that this is true not just for quadrilaterals, but for any polygon; the sum of the exterior angles is 360 degrees, regardless of the number of sides.  Thanks for asking, Chanchal!

"If the two triangles shown are similar, find the value of d/c. I know the answer is 5/6, but I don't know how to get it." ~Kimberly

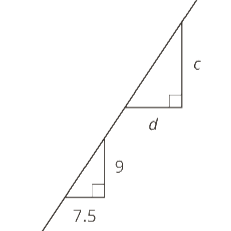
Good morning Kimberly. As we look at this question, I'd like to point out that it does violate one of our standard rules of geometry - which is that we never assume the diagrams are drawn to scale. The problem writer clearly intends for you to assume that the lines which appear to be horizontal really are horizontal, and the ones that appear to be vertical really are vertical. If you make that assumption, then you can conclude that the side of length 7.5 corresponds to the side of length d, and the side of length 9 corresponds to the side of length c. So we'll go with that assumption.

Since the triangles are similar, and we "know" which sides are corresponding, we can set up a ratio:

7.5/d = 9/c.

This does not give us what we want (d/c). However, we can rearrange that with just a couple steps to obtain the desired result. First multiply both sides by d, to get it in the numerator:

d(7.5/d) = d(9/c)
7.5 = 9d/c

Now divide both sides by 9:

7.5/9 = d/c

This is the ratio you want, except that it's not in simplest form. Multiply numerator and denominator by 2 in order to get rid of the decimal:

7.5/9 = 15/18 = 5/6.

And there's your answer. But I'm not quite done - I'd like to point out something that might be valuable to you. This problem shows us something very interesting that I often make use of when doing similar triangle problems.

We started with a ratio of corresponding sides, and when we were done, we ended with a very different ratio - the ratio of sides within a triangle.

Your standard rule is: The ratios of corresponding sides in two similar triangles are equal.

Our alternate version (which you can call the Kimberly Rule, if you want) is: The ratio of any two sides in a triangle is equal to the ratio of the corresponding sides in a second, similar triangle.

In other words, you could have started out with d/c = 7.5/9 instead of starting out with 7.5/d = 9/c. 

I had a student ask today why Cramer's Rule works. That's the sort of question I love, but we didn't have time in class to work through it, so I thought I'd post the exploration of the question here. We'll consider the case of a system of two equations in two unknowns.

Cramer's Rule says that if you have a system written as follows:

ax + cy = e
bx + dy = f

Then we can find the values of x and y by evaluating the following determinants.

In case you're not familiar with determinants, we find the value of a 2 x 2 determinant by multiplying the numbers along the primary diagonal (top-left to bottom-right) and then subtracting the product of the other diagonal. Thus, this could be rewritten as follows:

So that's the form we're going to consider. Ideally, we'd like to show that given the system we started with, the solutions can be written in the form directly above.

If you were solving a system of equations with numeric coefficients, you might find the least common multiple of the coefficients of x, and then figure out what you need to multiply each equation by in order to get those coefficients to cancel. Unfortunately, we don't have numeric coefficients, but we can still do this process. What is the LCM of a and b? Why, it's the product of a and b! So we'll multiply the first equation by b, and the second equation by -a:

 bax + bcy =  be
-bax - ady = -af

Adding these two equations gives us

bcy - ady = be - af 
y(bc - ad) = be - af    (factor out y)
y = (be - af)/(bc - ad)    (divide both sides by (bc + ad)

Now, that doesn't exacly match the result we expected, but if we multiply the top and the bottom by -1, we get:

y = (af - be)/(ad - bc)

That's only half of the problem, of course; we've shown that the "y" formula works; now we just need to show that the "x" formula works.

And you know what? We'd show it exactly the same way, except we'd start by eliminating y instead of x. I'll leave that to you to work out on your own. And, of course, once you've finished that, you can develop your own proof for systems of three equations in three unknowns!