Sixth grader Abdulla from U.A.E. asks the following question: "Are there perpendicular sides in trapezoid?"

The answer to that question, Abdulla, is "sometimes yes, sometimes no."

When people say the word "trapezoid," the image that automatically conjures up for most people looks like this:

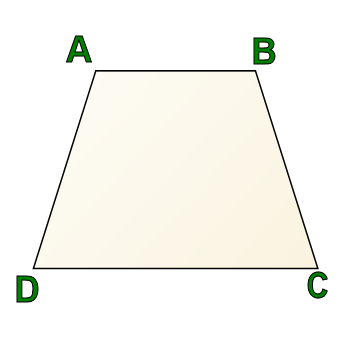
This is a trapezoid, and it is often described as a triangle with the top lopped off, or as a "dog food dish."

In this particular trapezoid, there are no perpendicular sides. A and B are both obtuse angles in this diagram, and C and D are both acute angles.

However, not all trapezoids look like this. Let's talk for a moment about the definition of a trapezoid.

Interestingly, the definition of "trapezoid" will vary depending on the part of the world in which you live, and in some parts of the world, the word "trapezium" is used for what I refer to as a trapezoid. I'm going to show you two definitions of trapezoid, and you'll need to check with your teacher/textbook to find out which way of defining a trapezoid is used in your part of the world.

Definition A: A trapezoid is any quadrilateral with exactly one pair of parallel sides.

Definition B: A trapezoid is any quadrilateral with at least one pair of parallel sides.

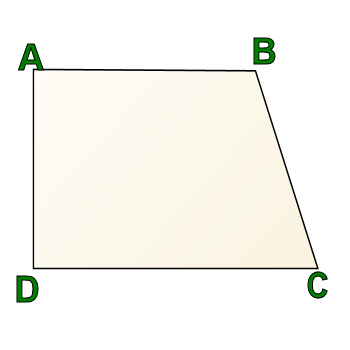
Regardless of which definition you use, the following is a trapezoid:

AB is parallel to CD still, so it meets definition B, and since AD is not parallel to BC, it also meets definition A.

This trapezoid is called a "right trapezoid." Why? Because always true of trapezoids (regardless of your definition): Right angles come in pairs in a trapezoid.

Why? Because

So this answers your question: Yes, some trapezoids have perpendicular sides.

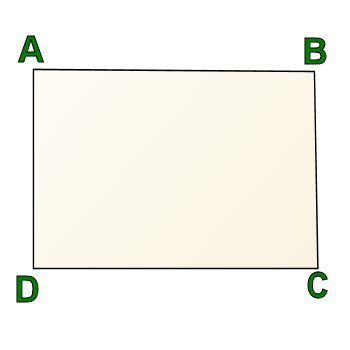
Let's take this one step further, though. Here's another figure. In this one, you have four right angles. That makes this a rectangle.

But is this figure also a trapezoid? It depends on whether you're using definition A or definition B.

If you're using definition A, it absolutely is not a trapezoid, because it has two pairs of parallel sides.

However, if you're using definition B, having two pairs of parallel sides is okay.

So if you're using definition B, then a trapezoid could be made up entirely of right angles, and a rectangle would be a special kind of trapezoid.

Otherwise, if you're using definition A, the most a trapezoid could have is two right angles, and therefore, two perpendicular sides.

Hope that helped answer your question!

Professor Puzzler

A visitor from Orlando asks:

"example of how to set up trapezoid ABCD, ABllCD, measure of interior angles are distinct and measure of

Well, there are a couple questions in here, one about an angle, and one about how to set up the trapezoid. Here's a picture that shows the setup of the trapezoid. Note that AB and CD are parallel, as the statement of the problem shows. Also note that the letters are in order around the vertices - from A to B to C to D, since the trapezoid is called ABCD. If the trapezoid had been named ACBD, we would have needed to rearrange our vertex names to match that.

We'll come back, in just a second, to the question of how to make sure the interior angle measures are distinct (all different).

But first the question is, how do we find the measure of angle A, if we know that the measure of angle D is x. If you've studied a bit of geometry, you may know that AD is a transversal between parallel lines AB and DC, and that interior angles A and D are consecutive interior angles, which is a fancy way of saying that they're on the same side of the transversal, between the two parallel lines. And consecutive interior angles are supplementary. This means they add to 180 degrees.

Therefore, m

m

m

As for how we make sure the angles are all distinct, there are two things we need to ensure.

First, we need to make sure that none of the angles are 90 degrees, because if ONE of them is 90 degrees, then the associated consecutive interior angle must also be 90 degrees, and that means the angle measures aren't all distinct. Thus, we can't have a right trapezoid.

The other thing is, we need to make sure it's not an isosceles trapezoid (AD = BC). If it's iscoseles, then m

Therefore, if the trapezoid is neither right nor isosceles, the angles will have distinct measures.

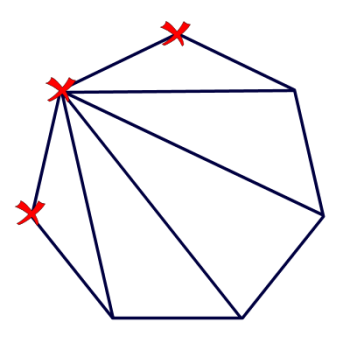
Ninth grader Michaela wants to know how you can "find the number of diagonals [in a polygon] drawn from a single vertex."

In answering this question, I'd like to point out that my diagram shows a convex polygon. If the polygon is concave, some of the diagonals will lie outside the polygon, but we would still call them diagonals.

If you look at the diagram to the right, you'll see that I've marked three vertices with an X.  Why? Because those are the vertices we can't draw a diagonal to.  You can't draw a diagonal from a vertex to itself, and you can't draw a diagonal from a vertex to its neighboring vertex. After all, drawing a line between two neighboring vertices isn't drawing a diagonal; it's drawing a side!

So, there are seven vertices in my polygon, and we can't draw diagonals to three of them, so that means we can draw diagonals to 7 - 3 = 4 vertices.

Can we generalize that? Of course! No matter how many sides the polygon has, there will always be 3 vertices you can't draw a diagonal to.

So if it has n vertices? You can draw n - 3 diagonals from any vertex.

As an added bonus (this goes beyond what you asked, Michaela!), this is how we get the formula for the number of diagonals in a polygon.

There are n vertices, and we can draw n - 3 diagonals from each one, making a total of n(n - 3) diagonals. Except...wait a minute! We've counted each diagonal TWICE (because we counted both endpoints!). So we need to divide that by two:

Total diagonals = n(n - 3)/2.

Enjoy your polygons!
Professor Puzzler

Question

Hi Professor Puzzler, I was wondering if you could explain what an axiom is?

Katie M, Grade 11
South Dakota

Answer

Hi Katie,

Well, I'm guessing that you're taking a Geometry class, because that's when many students first see that term.

An axiom is something that you believe or accept to be true without having ever proven it.  It is something that you consider to be "obviously true." You might not realize it, but your life is filled with axioms - things that have never been proven to you, but you believe anyway.  I once asked a group of high school students to name some things they couldn't prove, but they were confident of anyway.  Here were some of their answers:

• My parents love me.
• The sun will rise tomorrow.
• Gravity keeps me from falling out into space.
• There is a God.
• 1 + 1 = 2.

Why are axioms important? Because when you are proving something, there will always be fundamental building blocks of ideas that your proof is based on, and it's important to remember that the most fundamental building blocks are actually things you haven't proved at all.

In a way, an axiom is sort of like what the Bible says about faith: faith is the substance of things unseen.

Euclid had some axioms (or postulates), and one of his very important axioms was that if you have a line, and a point that's not on the line, there's only one line that goes through the point, and is parallel to the line.  That might seem obvious, but some other mathemeticians like Lobachevsky, Riemman, and Gauss had some different ideas, and their notions of geometry turned out to be very different from Euclid's.

The assumptions you start with can drastically change your results!

In modern usage, the "obviously true" concept is not how axioms are always viewed; in another sense, we could view an axiom as simply a "rule of the game" in mathematics.  In other words, mathematicians might say, "Let's start from assumption X, and see what sort of mathematics we develop!"  The assumption, or axiom they begin with may not be something that's "obviously true," but often valuable results come from such game playing.

Thanks for writing,
Professor Puzzler