Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
One student asks for an explanation of central angles - how is a central angle different from an inscribed angle?
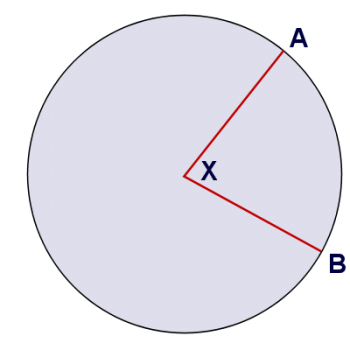
The best answer to this question is probably a picture (or, rather, a pair of pictures). The first picture shows a circle with center at X. The angle has its center at the center of the circle. Therefore, it's a central angle.
The second picture shows an additional angle, marked in green. This angle is an inscribed angle, because its vertex lies on the circle.
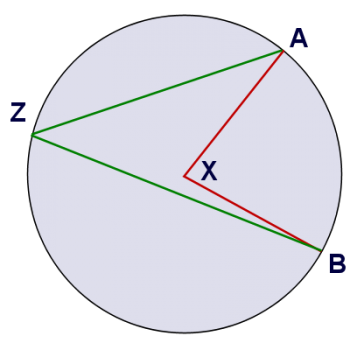
In both cases, the angles cut off the same arc - arc AB. So how are these two angles different? Well, if you look at the picture, you can see pretty easily that an inscribed angle is smaller than a central angle that cuts off the same arc. I think we can prove that the inscribed angle is half the size of the central angle. Want to give it a try?
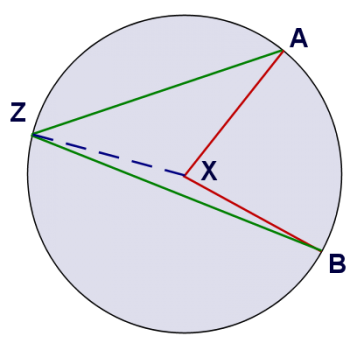
Let's construct a segment from Z to X, which splits the quadrilateral AXBZ into two triangles: AZX and BZX. Both of these triangles are isosceles (because two of their sides are radii of the circle). If we let m be the measure of angle AZX, n be the measure of angle BZX, and k be the measure of the central angle, then we can write the following equation for the sum of all the interior angles of the quadrilateral AXBZ:
(measure of AZB) + (measure of B) + (measure of A) + (measure of X) = 360
(m + n) + (n) + (m) + (360 - k) = 360
2m + 2n + 360 - k = 360
k = 2(m + n)
And since m + n is the measure of AZB, we've shown that the measure of a central angle has twice the measure of any inscribed angle that cuts the same arc. I hope that's helpful!


