Ask Professor Puzzler

Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!

Fractional Inequality

Posted by Professor Puzzler on October 12, 2017
Tags: math

How do you solve an inequality which looks like the following?

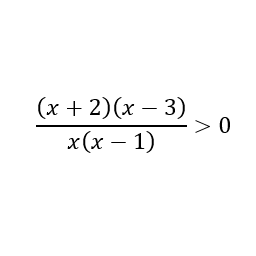
The expression on the left side of the sample equation is made up two factors in the numerator and two in the denominator. The key to solving this is recognizing that all that really matters is the sign of each individual factor. If all the factors are positive, the result is positive. If one of the factors is negative, then the result will be negative. If two of the factors are negative, the result is positive, and so forth. If the number of negative factors is even, the result is positive.

So we first need to find the points at which the different factors change sign, because those are the points at which the sign of the entire expression changes. We find these points of interest by setting each factor equal to zero (after all, the point at which the factor is zero is the point at which the factor is changing sign).

x + 2 = 0
x = -2

x - 3 = 0
x = 3

x = 0

x - 1 = 0
x = 1

So our points of interest are x = -2, x = 0, x = 1, and x = 3.

I listed those in ascending order; which will make it a little easier to finish up the problem.

If x < -2, then all the factors are negative, and the result is positive.

If -2 < x < 0, then x, (x - 1) and (x - 3) are negative, giving a negative result.

If 0 < x < 1, then (x - 1) and (x - 3) are negative, giving a positive result.

If 1 < x < 3, only (x - 3) is negative, giving a negative result.

If x > 3, none of the factors are negative, and the result is positive.

Thus, the solution is x < -2 or 0 < x < 1 or x > 3